Blog
Beiträge zu den Themen Biomedizin, Sozioökonomie und Finanzportfolios:
Mikrobiome - Von Reads zu Taxa | Mikrobiome - Visualisierung unds Statistik | Kombination von PhenoGraph und t-SNE | Dimensionsreduktion und Clustering am Beispiel von Durchflusszytometriedaten | Textanalyse - Wahlprogramme der Parteien zur Bundestagswahl | RDI- und Horizontplot | Kaufpreise von Wohnungen in Rostock | Benchmarking und Risikokennzahlen | Korrelation von Portfolio-Positionen | Preisverlauf und Charts von Portfolio‑Positionen | Kartendaten | Visualisierung von Daten unterschiedlicher Gruppen | Die Website geht an den Start
↓ zum ersten Eintrag
Mikrobiome - Visualisierung und Statistik
Datum: 04.02.2018
Vor-Filtern der Daten
Ein Grund für das Filtern ist es, Zeit für die Analyse von extrem seltenen Taxa einzusparen. “Selten” kann sich dabei sowohl auf die Abundanz (z.B. “Taxa macht 10% aller ”Reads" in einer Probe aus“) als auch auf die Prävalenz (z.B. ”Taxa kommt in 20% aller Proben vor“) beziehen. Für welche Analysen man wenig abundante bzw. prävalente Taxa herausfiltert, sollte man sich vorher gut überlegen. Zum Einen kann man Rauschen aus den Daten herausfiltern (z.B. Artefakte des bisherigen Untersuchungsprozesses). Auf der anderen Seite kann man die Diversität der Probe unterschätzen.
Der Zusammenhang zwischen Prävalenz und Abundanz für jede Amplikon Sequenzvariante (ASV) bietet häufig einen Anhaltspunkt, um Ausreißer zu finden oder bietet Informationen über die Bereiche dieser beiden Parameter, die für die sich anschließenden Analysen notwendig sind.

Abundanzen
Abundanzen können absolut und relativ betrachtet werden. Die absolute Abundanz bezieht sich auf die Anzahl der gemessenen Sequenzen einer ASV in einer Probe. Vergleicht man verschiedene Proben miteinander, so können diese allerdings stark variieren. Dies kommt daher, dass technisch bedingt die Gesamtzahl der gemessenen Sequenzen von Probe zu Probe unterschiedlich ist. Möchte man die Abundanzen zwischen zwei Proben vergleichen, muss man sich also auf relative Abundanzen beziehen. Diese ermittelt man, indem man die absolute Abundanz durch die Gesamtzahl der gemessenen Sequenzen in dieser Probe teilt. Die relativen Abundanzen einer Probe summieren sich dann auf den Wert Eins. Der Nachteil der relativen Abundanzen ist allerdings, dass man Information über die Sequenziertiefe, also die insgesamt gemessenen Sequenzen verliert. Auch hier muss man sich je nach Fragestellung und Analysemethode entscheiden, was man verwendet.
Stacked-barplots
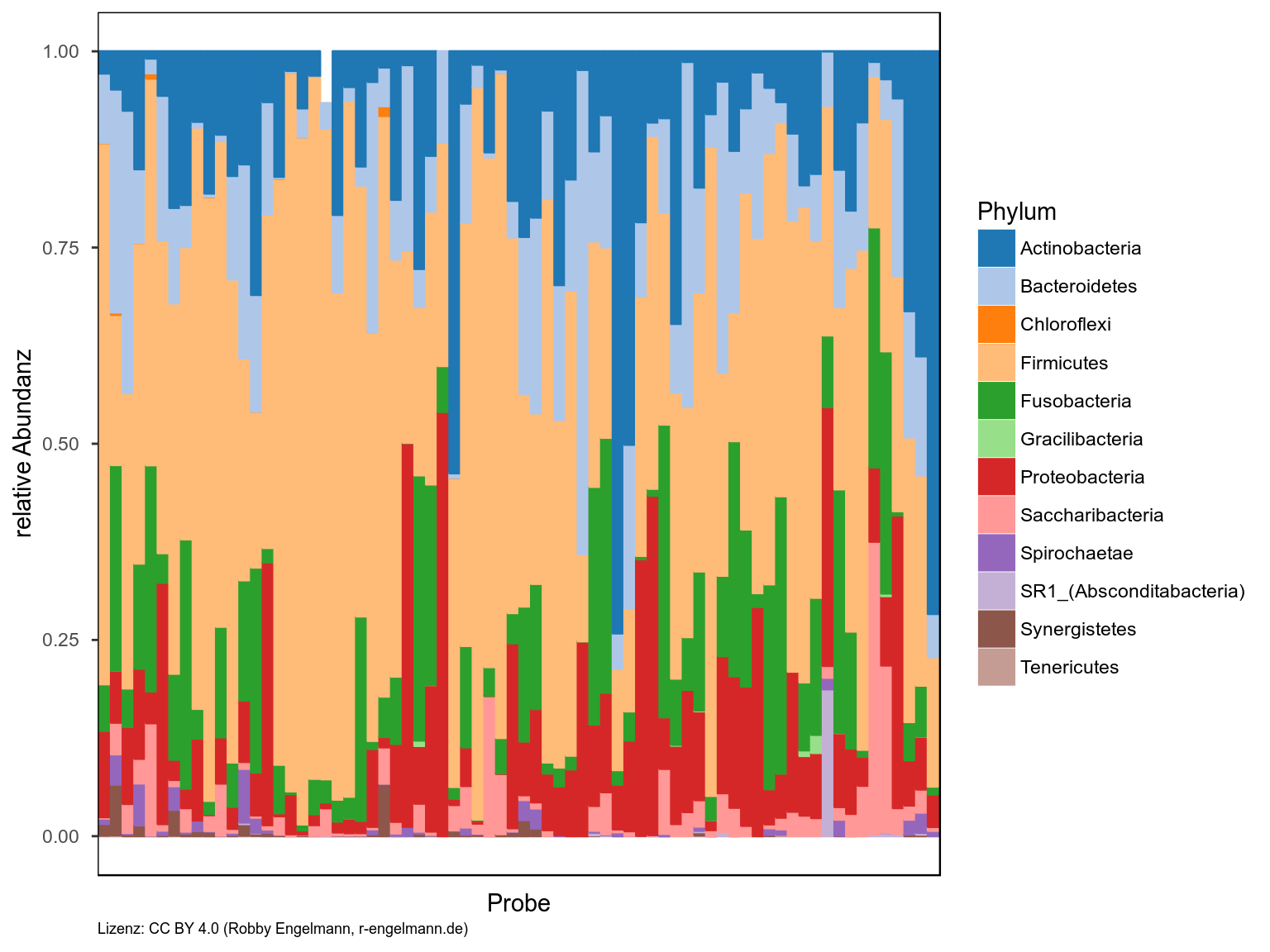
Die Abundanz lässt sich mit verschiedenen Darstellungsformen visualisieren. Als erstes Beispiel habe ich hier das gestapelte Balkendiagramm (engl.: stacked-bars) gewählt. Die erste Version zeigt jede Probe der Studie einzeln. In der zweiten Abbildung wurden alle Proben eines Entnahmeortes gemittelt dargestellt. In den Abbildungen bedeuten Tongue = Zunge, Subg = subgingival (Beläge auf dem Zahn unterhalb des Zahnfleischrandes aus der Zahntasche) und Supra = supragingival (Beläge auf dem Zahn über dem Zahnfleischrand). Die einzelnen Elemente des Balkenstapels spiegeln die jeweiligen Abteilungen (Phylum) wieder. Man könnte hier natürlich auch eine andere taxonomische Stufe wählen oder sich z.B. auf die Gattungen einer Abteilung beschränken.

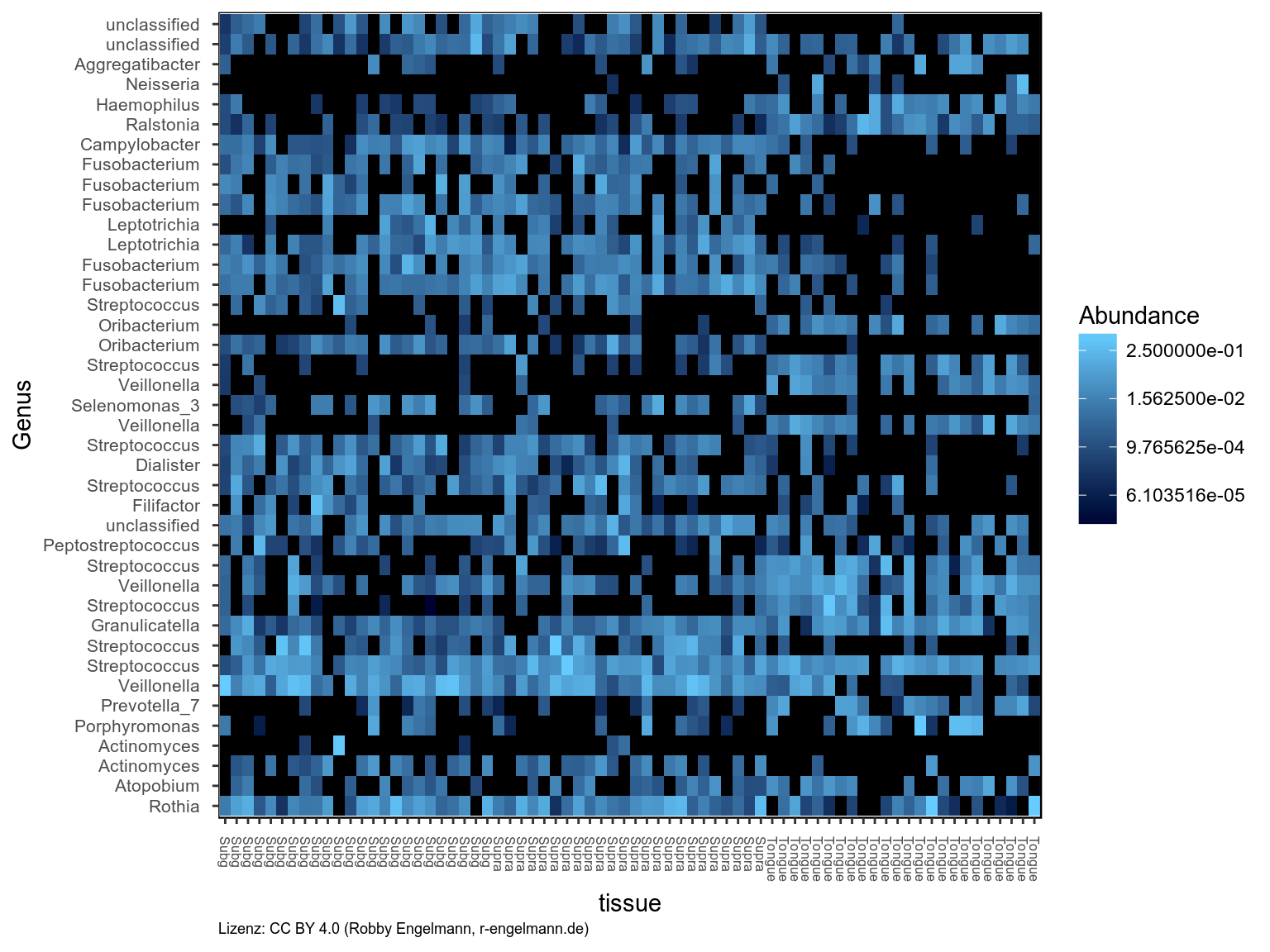
Heatmap
Als nächstes wurden die 40 ASVs mit der höchsten relativen Abundanz gefiltert und die Heatmap als Darstellungsform gewählt. Hier kann man Taxa ablesen, die kaum auf der Zunge wohl aber in den Zahnbelägen vertreten sind (dunkler Bereich rechts oben). Außerdem kann man Taxa erkennen, die kaum in den Zahnbelägen, wohl aber auf der Zunge zu finden sind (dunkler Bereich links in der Mitte).
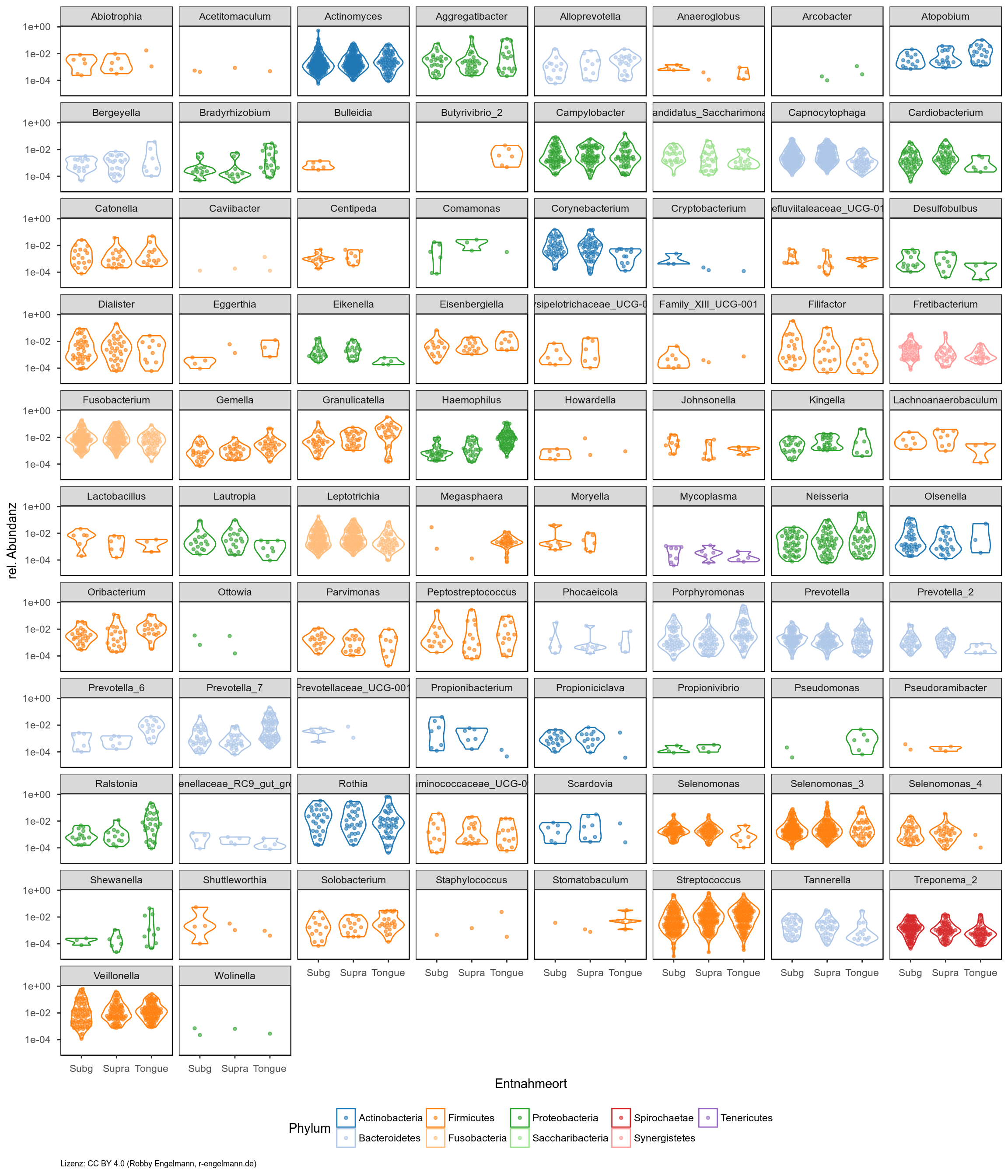
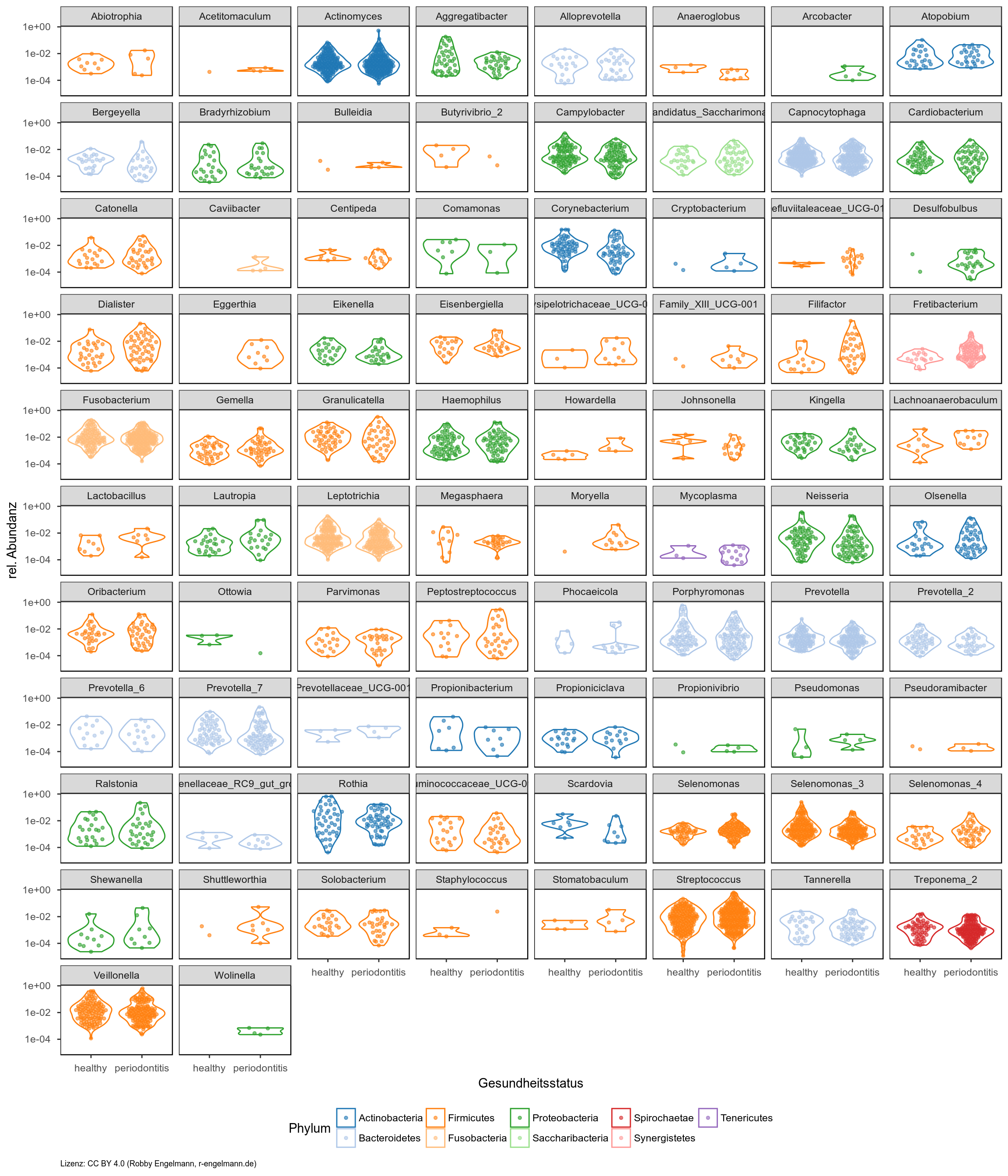
Gruppenvergleiche
Die folgenden Grafiken bieten einen schnellen Überblick über die Unterschiede zwischen verschiedenen Gruppen. Man sieht für alle zugeordneten Gattungen die relativen Abundanzen vergleichend für Entnahmeorte (erste Grafik) bzw. den Gesundheitsstatus (gesund versus Parodontitis in der zweiten Grafik) auf der y-Achse. Die Anzahl der Punkte gibt außerdem die Unterschiede in der Prävalenz wieder.
Treeplot
Dargestellt ist der Abstammungsbaum der ASVs aus den Gattungen Haemophilus und Tannerella. An den Spitzen des Baumes (den Blättern) ist je Probe ein Punkt dargestellt, wobei die Größe des Punktes die Abundanz wiedergibt und die Farbe beschreibt aus welcher Entnahmestelle die Probe entstammte.
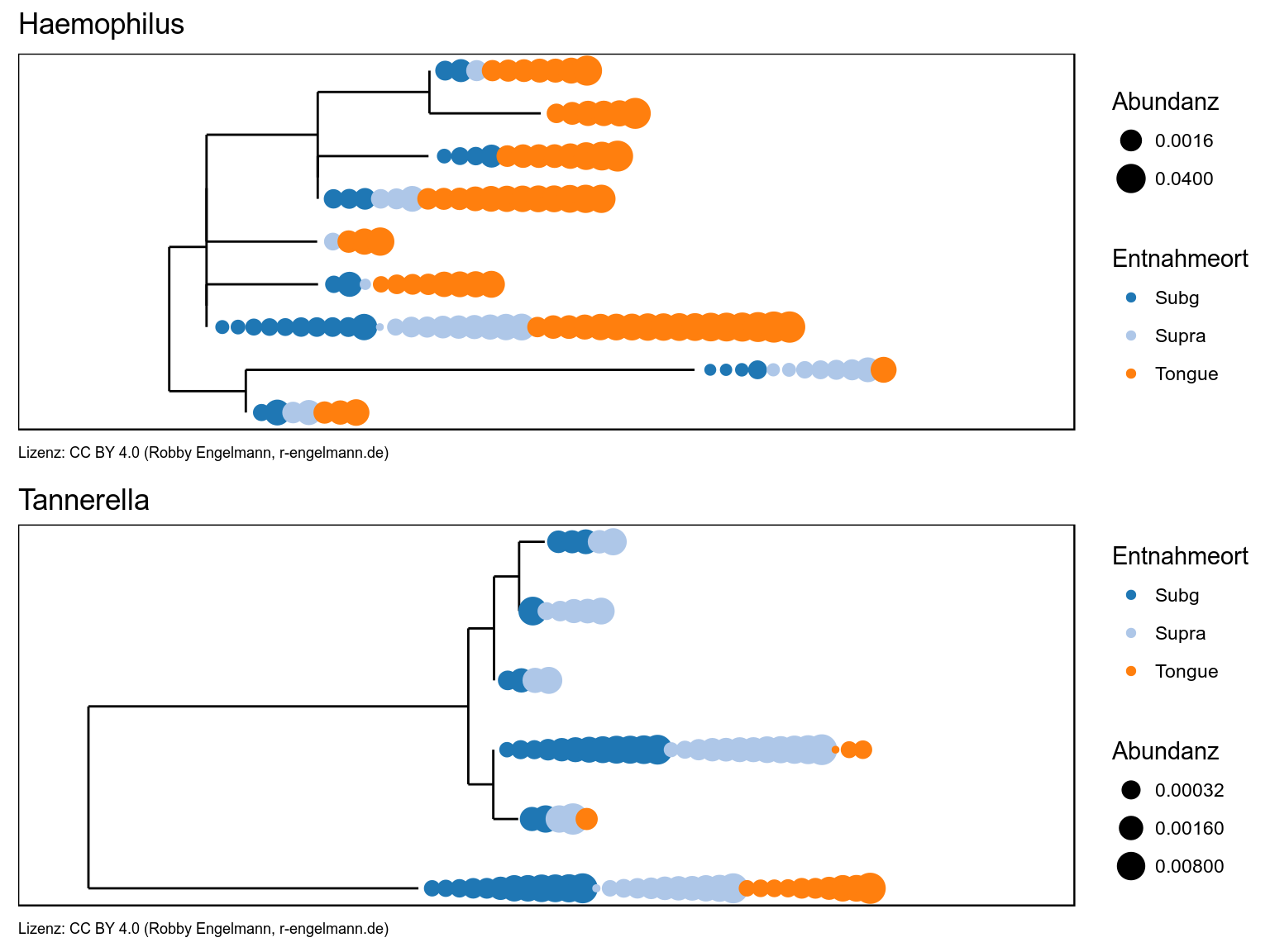
Diversität
alpha-Diversität
Die alpha-Diversität beschreibt die Anzahl bzw. Verteilung der Taxa innerhalb eines Lebensraumes. Bei der Mikrobiomanalyse bedeutet dies, wie viele verschiedene Taxa in einer Probe zu finden sind und wie deren Abundanzen verteilt sind. Ein Vergleich der alpha-Diversität verschiedener Proben ist nur statthaft, wenn alle Proben den gleichen Umfang haben.
Für die alpha-Diversität gibt es eine große Auswahl an Maßen. Allen gemein ist, dass man etwaige Unterschiede in der Anzahl an Reads zwischen den zu vergleichenden Proben ausgleichen muss. Eine Herangehensweise ist, dass man aus jeder Probe nur die Anzahl an Reads zieht, die in der Probe mit der geringsten Anzahl vorhanden sind. Dies wiederholt man einige Male und mittelt das Ergebnis.
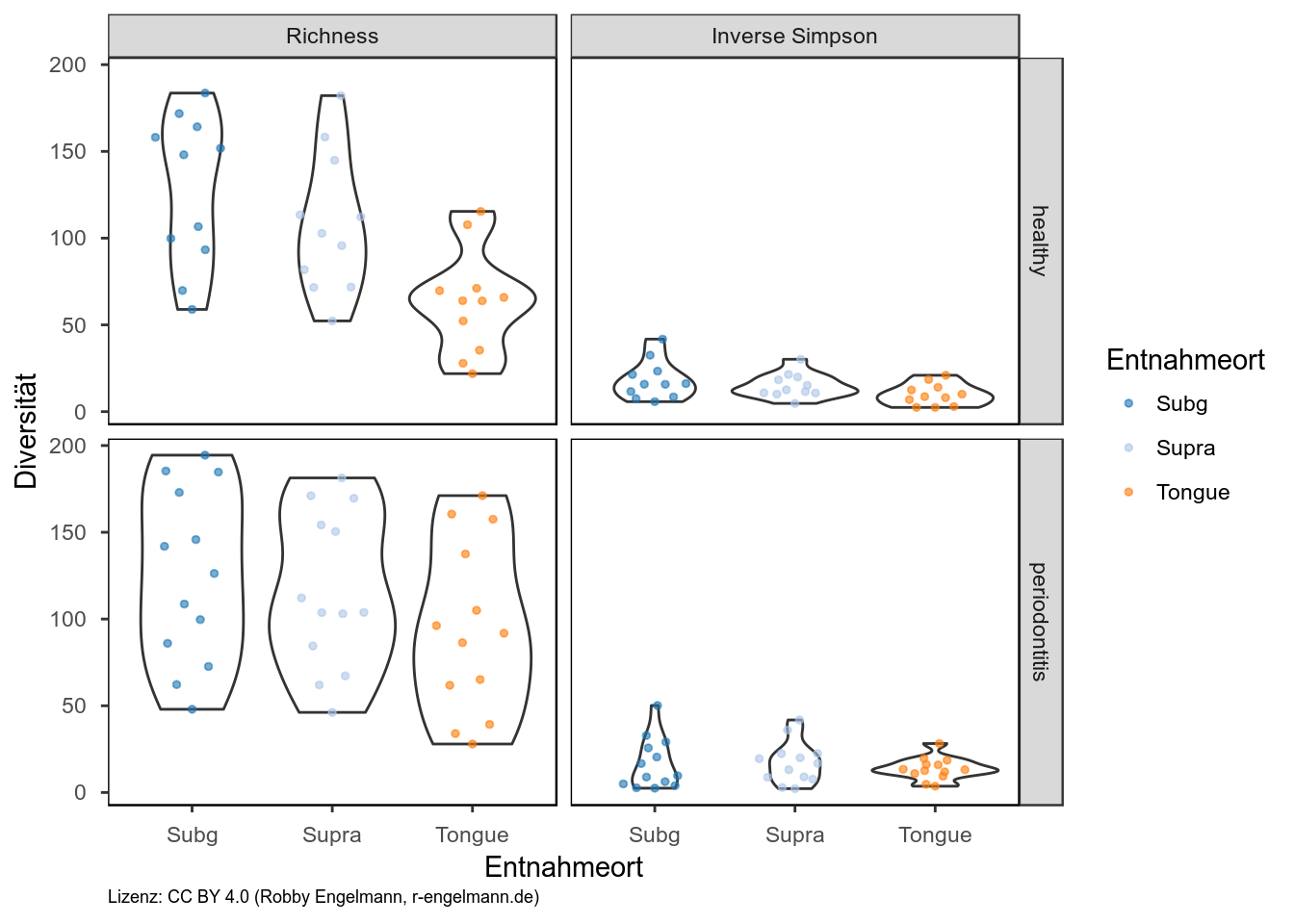
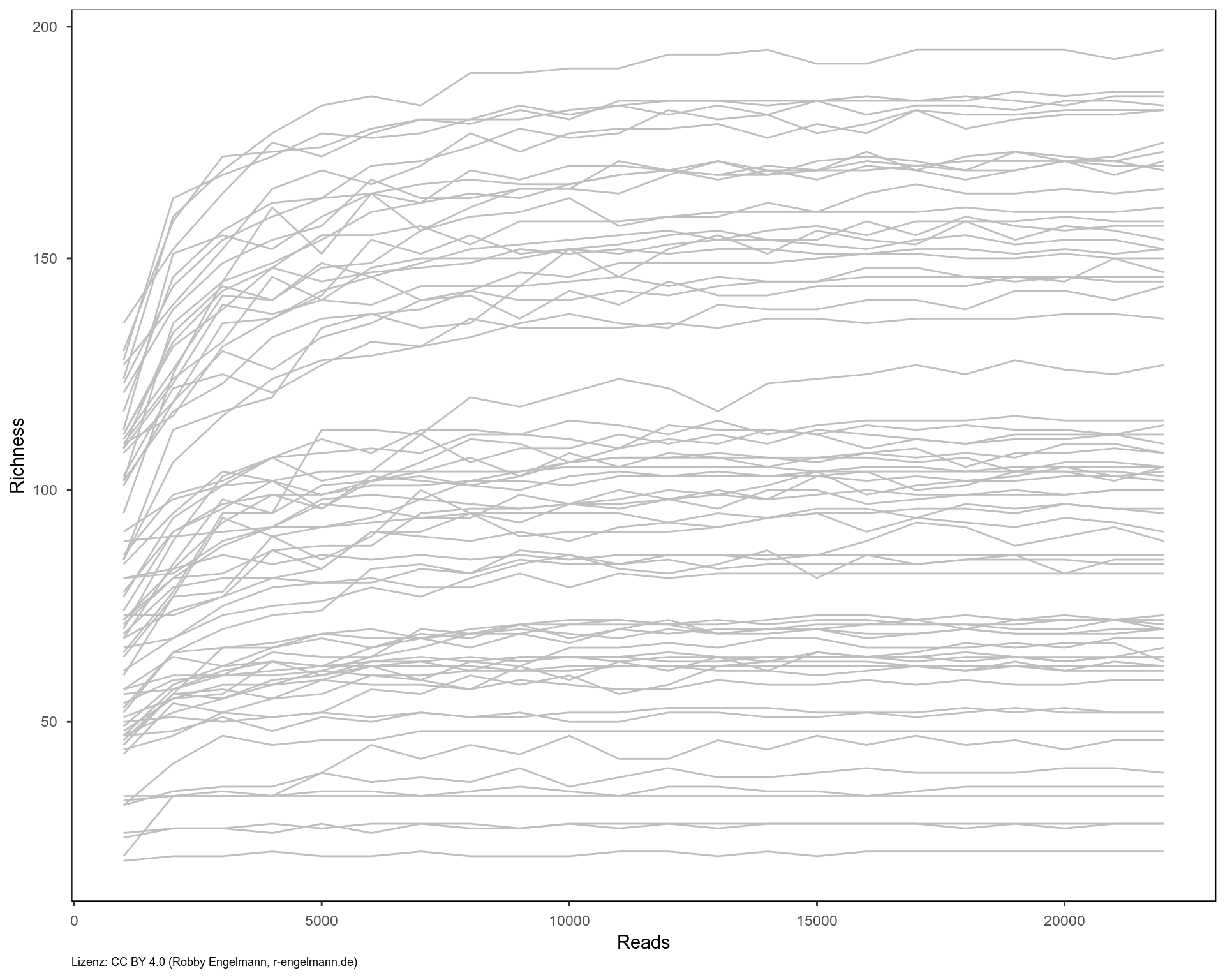
Wichtig dabei ist es zu überprüfen, ob die verwendete Anzahl an Reads ausreicht, um sich dem tatsächlichen Wert für die alpha-Diversität anzunähern, oder ob man die Diversität unterschätzt, weil zu wenige Reads gemessen wurden. Dies kann man prüfen, indem man eine steigende Anzahl an Reads aus den Proben zieht und das jeweilige Diversitätsmaß bestimmt. Die Diversität sollte sich mit steigender Readzahl der tatsächlichen Diversität annähern. Steigt die Kurve bei der gemessenen Readzahl noch immer an, so unterschätzt man die Diversität, weil keine ausreichende Menge an Daten vorliegt.
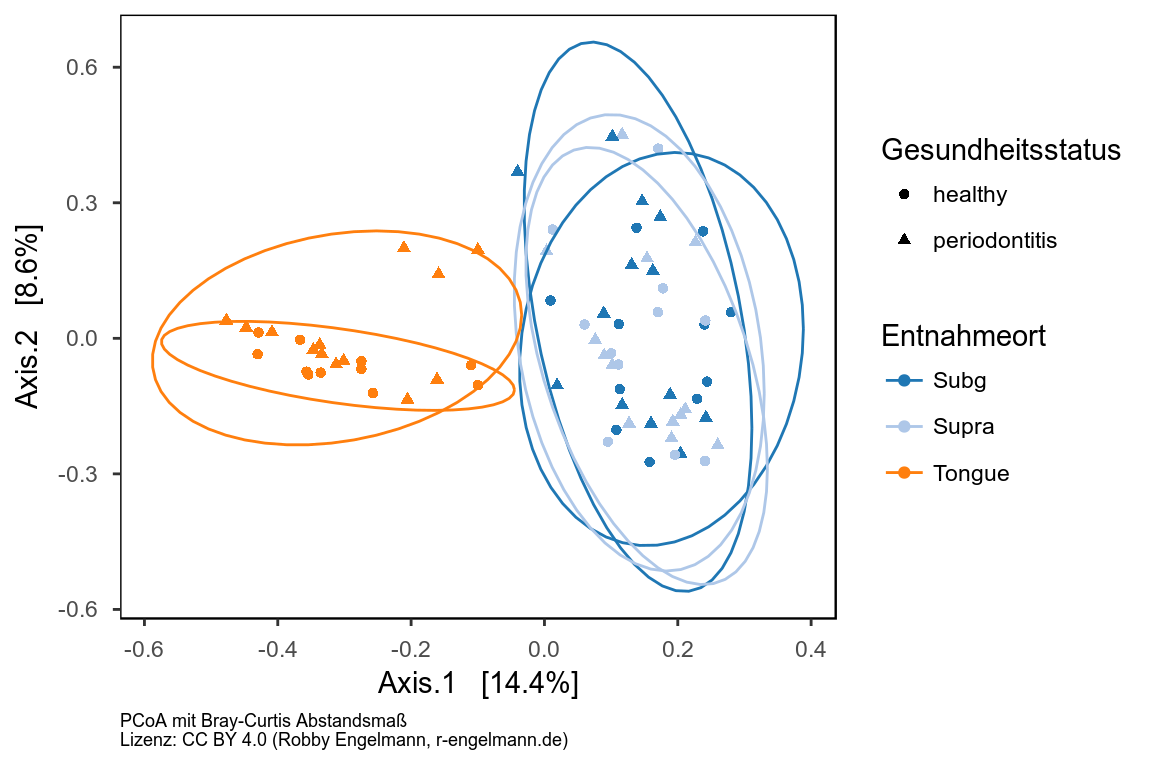
beta-Diversität
Die beta-Diversität beschreibt die Diversität der Mikrobiota zwischen verschiedenen Lebensräumen. Bei der Mikrobiomanalyse bedeutet dies, zu untersuchen, ob und wie sich die mikrobiotische Zusammensetzung von einer zur anderen Probe unterscheidet.
Zur Untersuchung der beta-Diversität werden standardmäßig verschiedene Methoden der Dimensionsreduktion (Principal Coordination Analysis [PCoA], Nonmetric multidimensional scaling [NMDS], u.a.) kombiniert mit unterschiedlichen Abstands- bzw. Unähnlichkeitsmaßen, die sich aus der Mikrobiom-Zusammensetzung der jeweiligen Proben ergeben (Bray-Curtis, Jaccard, (un)gewichtete UniFrac). Drei Beispiele folgen hier.
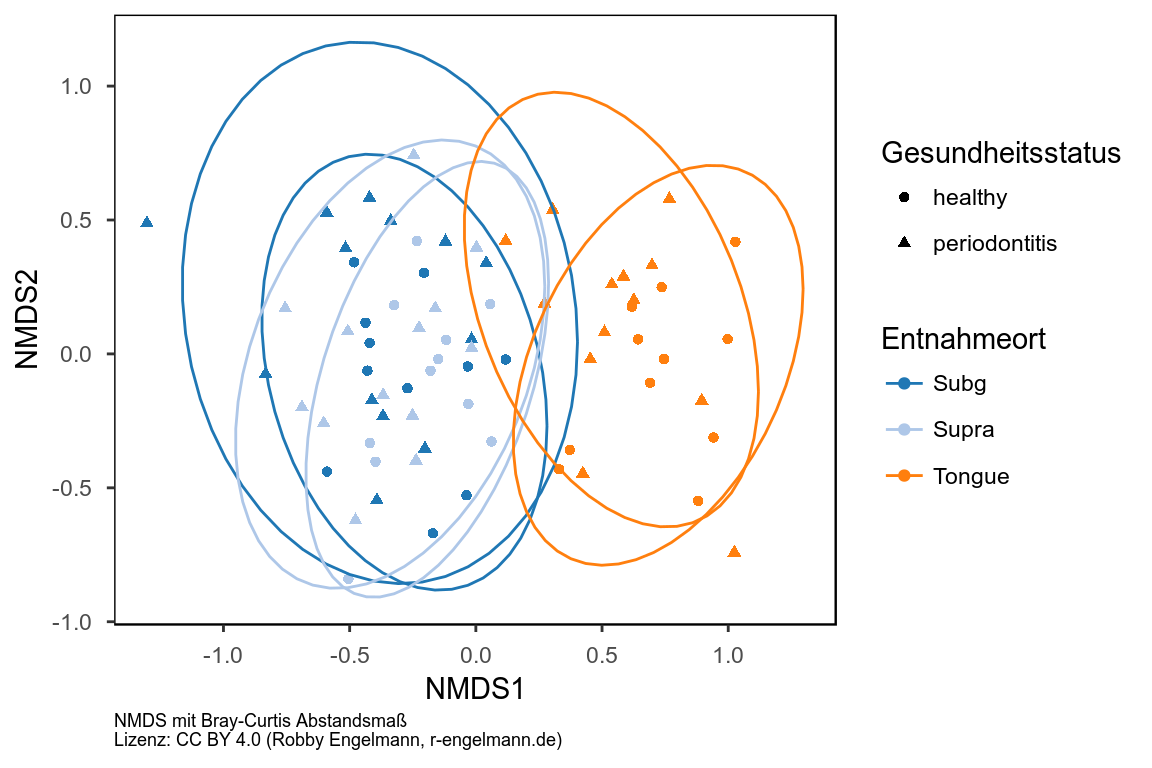
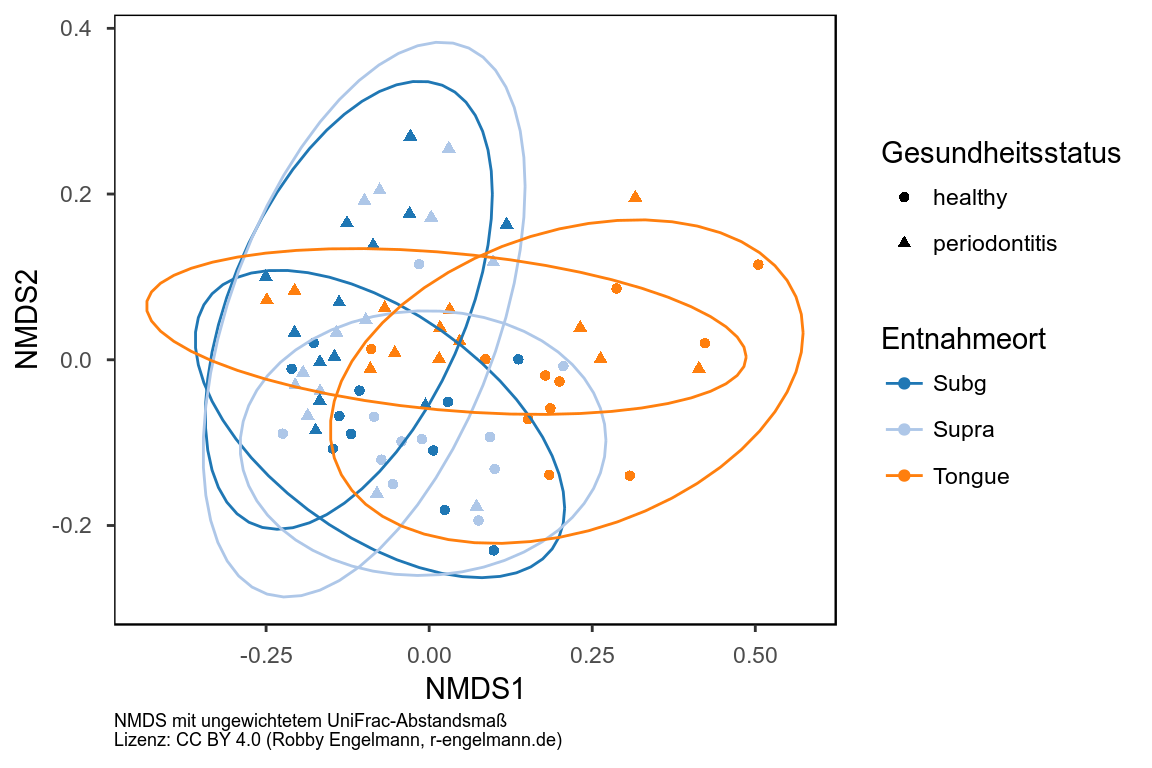
Gemeinsames Auftreten von ASVs
Eine weitere Fragestellung ist die des gemeinsamen Auftretens bestimmter Taxa an einem Ort. Für diese Analyse bietet das R-Paket “cooccur” einige Ansätze, auf die hier allerdings nicht näher eingegangen werden soll. Als Visualisierung für das gemeinsame Auftreten bieten sich Netzwerke an.
Statistik
Mikrobiomdaten sind durch statistische Eigenschaften gekennzeichnet, die die Anwendung einiger Standardmethoden und -modelle ausschließt:
- Gesamtzahl an Reads kann substantiell von Probe zu Probe schwanken
- Homoskedastizität (Unabhängigkeit der Varianz von den Faktorwerten) ist nicht vorliegend, jedoch Voraussetzung für die Anwendung vieler parametrischer aber auch nicht-parametrischer Tests
- keine Normalverteilung der Daten (Abundanzmatrix mit eher diskreten Werten und vielen Nullen)
Welche statistischen Verfahren Anwendung finden können, kann man zusammenfassend in “Odintsova V, Tyakht A, Alexeev D. Guidelines to Statistical Analysis of Microbial Composition Data Inferred from Metagenomic Sequencing. Current Issues in Molecular Biology. 2017; 17–36.” nachlesen. Hier nur ein paar wenige Stichworte: PERMANOVA, ANOSIM und generalisierte lineare Modelle.
Für die genaue Beschreibung der anwendbaren statistischen Methoden sei an dieser Stelle auch auf die unten genannten wissenschaftlichen Publikationen verwiesen.
Referenzen
Datenquellen
wissenschaftliche Publikationen
- Buttigieg PL, Ramette A. A guide to statistical analysis in microbial ecology: a community-focused, living review of multivariate data analyses. FEMS Microbiol Ecol. 2014;90: 543–550. doi:10.1111/1574-6941.12437
- FUKUYAMA J, MCMURDIE PJ, DETHLEFSEN L, RELMAN DA, HOLMES S. COMPARISONS OF DISTANCE METHODS FOR COMBINING COVARIATES AND ABUNDANCES IN MICROBIOME STUDIES. Pac Symp Biocomput. 2012; 213–224.
- Griffith DM, Veech JA, Marsh CJ. cooccur: Probabilistic Species Co-Occurrence Analysis in R. Journal of Statistical Software. 2016;69. doi:10.18637/jss.v069.c02
- Lozupone C, Knight R. UniFrac: a New Phylogenetic Method for Comparing Microbial Communities. Appl Environ Microbiol. 2005;71: 8228–8235. doi:10.1128/AEM.71.12.8228-8235.2005
- Odintsova V, Tyakht A, Alexeev D. Guidelines to Statistical Analysis of Microbial Composition Data Inferred from Metagenomic Sequencing. Current Issues in Molecular Biology. 2017; 17–36. doi:10.21775/cimb.024.017
- Paulson JN, Pop M, Bravo HC. metagenomeSeq: Statistical analysis for sparse high-throughput sequencing. Bioconductor package. 2013;1.
- Xia Y, Sun J. Hypothesis testing and statistical analysis of microbiome. Genes & Diseases. 2017;4: 138–148. doi:10.1016/j.gendis.2017.06.001
- Zhu X, Wang J, Reyes-Gibby C, Shete S. Processing and Analyzing Human Microbiome Data. In: Elston RC, editor. Statistical Human Genetics. New York, NY: Springer New York; 2017. pp. 649–677. doi:10.1007/978-1-4939-7274-6_31
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.4.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 17.12.0 (entwickelt von der KDE Community) http://kate-editor.org
- phyloseq: An R package for reproducible interactive analysis and graphics of microbiome census data. Paul J. McMurdie and Susan Holmes (2013) PLoS ONE 8(4):e61217.
- Leo Lahti et al. microbiome R package. URL: http://microbiome.github.io
- Jari Oksanen, F. Guillaume Blanchet, Michael Friendly, Roeland Kindt, Pierre Legendre, Dan McGlinn, Peter R. Minchin, R. B. O’Hara, Gavin L. Simpson, Peter Solymos, M. Henry H. Stevens, Eduard Szoecs and Helene Wagner (2018). vegan: Community Ecology Package. R package version 2.4-6. https://CRAN.R-project.org/package=vegan
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.2.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Erik Clarke and Scott Sherrill-Mix (2017). ggbeeswarm: Categorical Scatter (Violin Point) Plots. R package version 0.6.0. https://CRAN.R-project.org/package=ggbeeswarm
- Claus O. Wilke (2017). cowplot: Streamlined Plot Theme and Plot Annotations for ‘ggplot2’. R package version 0.9.2. https://CRAN.R-project.org/package=cowplot
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- Simon Garnier (2017). viridis: Default Color Maps from ‘matplotlib’. R package version 0.4.0. https://CRAN.R-project.org/package=viridis
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.8 https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
Mikrobiome - Von Reads zu Taxa
Datum: 04.02.2018
Mikrobiome
Was?
Das Mikrobiom bezeichnet alle auf oder in einem Organismus lebenden Mikroorganismen. Typischerweise untersucht man das Mikrobiom von bestimmten Körperbereichen (Magen-Darm-Trakt, Mundhöhle usw.), die man für seine wissenschaftliche Fragestellung als relevant betrachtet.
Wozu?
Warum ist es von Interesse sich die Zusammensetzung der auf uns lebenden Mikroorganismen anzuschauen? Wie wir heute wissen, spielt die Zusammensetzung der Mikroorganismen u.a. eine Rolle bei:
- der Anfälligkeit für eine Vielzahl an Erkrankungen (Krebs, Herz-Kreislauf-Erkrankungen, Infektionen und vielen weiteren)
- Ansprechen auf Behandlungen (Wie verstoffwechselt der Körper bestimmte Medikamente?)
Die genauen Zusammenhänge sind zum großen Teil noch unbekannt. Die Techniken zur Untersuchung des Mikrobioms entwickeln sich derzeit zwar rasant, dennoch kratzt man gerade mal an der Oberfläche und betreibt manchmal auch etwas Kaffeesatzleserei.
Wie?
Als erstes ist es notwendig das genetische Material der Mikroorganismen zu gewinnen. Soll beispielsweise das Mikrobiom des Darms untersucht werden, isoliert man das genetische Material aus einer Stuhlprobe. Es wird angenommen, dass diese dann auch das genetische Material aller vorkommenden Bakterien enthält. Zunächst werden definierte Bereiche der Mikroben-DNA vermehrt, die die genetische Information für bestimmte variable Abschnitte der 16S-rRNA der Bakterien enthält. Von diesen vervielfältigten DNA-Bereichen wird die Basenabfolge bestimmt. Am Ende erhält man eine große Sammlung (=Library) von einzelnen Basensequenzen der DNA (=Reads), aus der auf die vorhandenen Bakterienspezies geschlossen werden kann, indem diese mit den Sequenzen bekannter Bakteriengruppen (=Taxa) verglichen werden.
Die Schritte von den Reads zu den Taxa
De-Multiplexen
Wenn man sehr viele Proben untersuchen will, so kann man das genetische Material jeder Probe mit einer einzigartigen genetischen Markierung versehen (=Barcode). Danach sequenziert man das Gemisch aus vielen Proben in einem einzelnen Sequenzier-Durchlauf. Dies spart Zeit und Geld. Allerdings muss man jede erhaltene Sequenz wieder der jeweiligen Ursprungsprobe zuordnen. Dies bezeichnet man als De-Multiplexing.
Entfernen von Barcodes, Primersequenzen, Linkern usw.
Die Sequenzen können nun noch die Barcodes und weitere DNA-Sequenzen enthalten, die nicht auf die Bakterien zurückgehen, sondern notwendigerweise bei der Vervielfältigung des Ausgangsmaterials eingebaut werden. Diese Sequenzbereiche müssen vor der Analyse entfernt werden.
Daten einlesen
Die Ausgangsdaten sind dann je Probe zwei fastq-Dateien (Textdateien mit den Sequenzen). Es sind zwei Dateien, da man je Probe bei der PCR sowohl sogenannte forward- als auch reverse-Stränge erhält, da beide Stränge der DNA-Doppelhelix vervielfältigt werden. Beide werden sequenziert und im Laufe des Workflows auch wieder zusammengefügt.
Im Blog hier möchte ich einem bereits publizierten Ablauf folgen und diesen auf Sequenzdaten aus einer Publikation anwenden, in der die Autoren Proben aus der Mundhöhle von Patienten mit Parodontitis und gesunden Probanden untersucht haben. Am Ende möchte ich die bereits publizierten Ergebnisse mit meinen eigenen Ergebnissen vergleichen.
Trimmen und Filtern der Rohsequenzen
Aufgrund der Sequenziertechnik besitzen nicht alle Sequenzen bzw. alle Sequenzbereiche eine hohe Qualität. Daher müssen die Reads zunächst entsprechend eingekürzt werden. Außerdem müssen Sequenzen geringer Qualität entfernt werden. Dazu besitzen die fastq-Dateien, die die Rohdaten enthalten, Informationen zur Fehlerwahrscheinlichkeit bzw. Qualität für jede Basenposition jedes Reads.
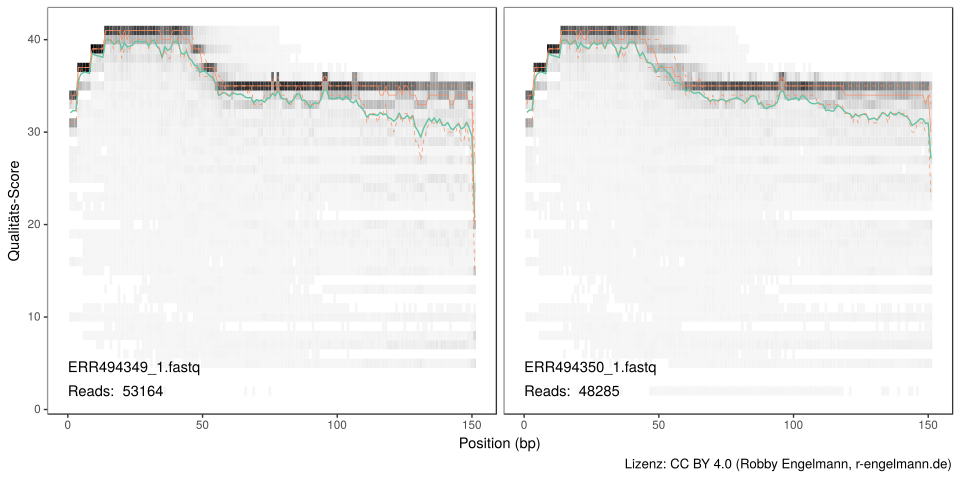
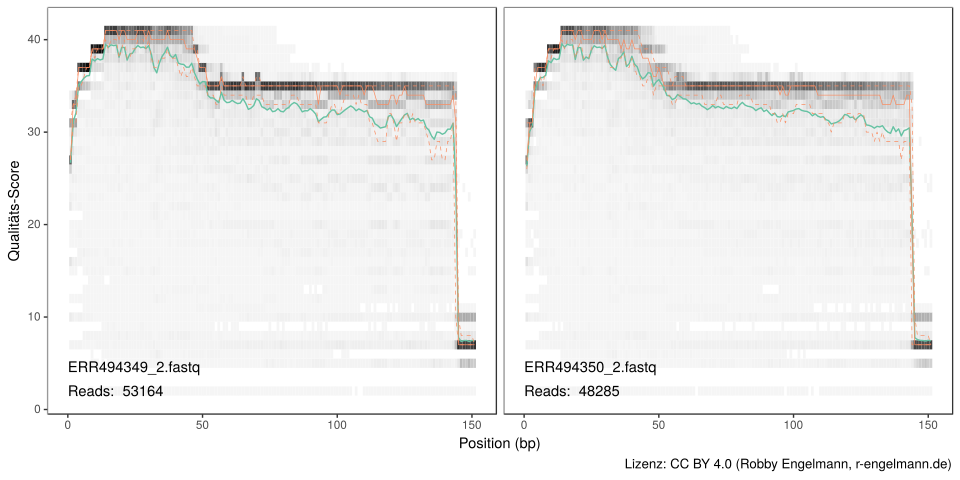
Wie man in den beiden Abbildung oben sieht, fällt die Qualität der Reads ab einer bestimmten Position stark ab. Daher trimmen wir die forward Reads ab Position 140 und die reverse Reads ab Position 135. Wir trimmen auch die ersten 10 Nukleotide jedes Reads basierend auf der Beobachtung, dass viele Illumina Datensätze an diesen Positionen besonders häufig Fehler enthalten. Dies sehen wir auch hier. Außerdem werden Sequenzen mit mehr als zwei erwarteten Fehlern pro Read gefiltert (Edgar und Flyvbjerg 2015). Das Trimmen und Filtern wird auf die gepaarten Reads gemeinsam angewendet, d.h. beide Reads müssen den Filter passieren, damit das Sequenzpaar erhalten bleibt.
Nach dem Filtern und Trimmen folgt typischerweise das zuordnen der Reads zu sogenannten OTUs (operational taxonomic units). Dies sind Gruppen von Reads, die sich weniger als eine festgelegte Schwelle unterscheiden (zumeist 97%). Hier nutzen wir stattdessen die DADA2-Methode, um die Amplikon Sequenzvarianten (ASVs) exakt zu bestimmen. Dabei wird kein willkürlicher Schwellenwert festgelegt und selbst Varianten mit nur einem Nukleotid Unterschied erkannt (Callahan et al.).
Sequenzvarianten aus den vorverarbeiteten Rohsequenzen ableiten
Für die hier verwendete DADA2-Methode sind einige Vorteile im Vergleich zu anderen Herangehensweisen (Mother, QIME, u.a.) beschrieben:
- Auflösung: DADA2 leitet aus den Reads genaue ASVs mit einer Auflösung von bis zu 1 oder 2 Nukleotiden ab.
- Genauigkeit: DADA2 gibt weniger falsch-positive Sequenzvarianten zurück als andere Methoden falsch-positive OTUs. DADA2’s entscheidender Vorteil ist, dass mehr Informationen in den Daten genutzt werden als bei anderen Methoden. Das DADA2 Fehlermodell bezieht Qualitätsinformationen mit ein, die bei allen anderen Methoden nach dem Filtern ignoriert werden. Das DADA2 Fehlermodell betrachtet außerdem quantitative Abundanzen, wohingegen die meisten anderen Methoden höchsten Abundanzränge mit einbeziehen. Das DADA2 Fehlermodell identifiziert auch die Unterschiede zwischen den Sequenzen (z.B. A->C), während andere Methoden lediglich die Mismatches zählen. Außerdem kann DADA2 die Parameter für sein Fehlermodell aus den Daten selbst ableiten, anstatt von vorigen Datensätzen abhängig zu sein, die nicht notwendigerweise die PCR und Sequenzierprotokolle abbilden, die man selbst nutzt.
- Vergleichbarkeit: Die ASVs von DADA2 können direkt zwischen verschiedenen Studien verglichen werden, ohne die Notwendigkeit die gepoolten Daten erneut zu analysieren, wie es bei der Nutzung von OTUs der Fall ist. Die nächste Abbildung zeigt das DADA2 Fehlermodell der hier verarbeiteten Daten.
- Skalierbarkeit: Die Berechnungszeit von DADA2 skaliert linear mit der Probenanzahl und der Speicherbedarf ist vergleichsweise niedrig. DADA2’s Verbesserung in der Skalierbarkeit basiert darauf, dass ASVs und nicht OTUs konstruiert werden müssen, denn für die Berechnung der OTUs müssen alle Proben gepoolt werden. Die exakten Sequenzen sind dagegen zwischen Proben vergleichbar, da diese genauen “Labels” entsprechen. Daher kann DADA2 jede Probe unabhängig analysieren, was zu einer linearen Skalierbarkeit mit steigender Probenzahl und trivialer Parallelisierung führt.
- Open Source: DADA2 ist unter der LGPL Version 3 lizensiert.

Sequenztabelle konstruieren
Jetzt werden die abgeleiteten forward- und reverse-Sequenzen zu jeweils einer Sequenz vereinigt. Dabei werden gepaarte Sequenzen, die nicht perfekt zusammenpassen, als letzte Kontrolle gegen verbleibende Fehler, entfernt. Als Ergebnis erhält man die entsprechenden ASVs und wie häufig sie jeweils vorkommen.
Chimäre Sequenzen entfernen
Aus der Sequenztabelle werden nun noch chimäre Sequenzen entfernt. Dies sind Sequenzen, die Teile aus verschiedenen Bakterienspezies enthalten. Diese können bei der PCR entstehen und sind technische Artefakte.
Analyseschritte prüfen
| ERR494349_1.fastq |
53164 |
45679 |
45679 |
44904 |
43584 |
| ERR494350_1.fastq |
48285 |
41715 |
41715 |
40042 |
37012 |
| ERR494351_1.fastq |
47321 |
39625 |
39625 |
38759 |
37531 |
| ERR494352_1.fastq |
39409 |
33109 |
33109 |
32306 |
31814 |
| ERR494353_1.fastq |
54830 |
46673 |
46673 |
46594 |
46594 |
| ERR494354_1.fastq |
46802 |
40456 |
40456 |
39571 |
37363 |
Taxonomie hinzufügen
Bisher haben wir ja noch keine Bakteriengruppen, sondern nur die Sequenzen, die zu bestimmten Bakteriengruppen gehören. Welche Bakteriengruppen bzw. -spezies das sind erhält man durch den Abgleich mit bestehenden Datenbanken. Hier wurde z.B. die SILVA-Datenbank (Version 128) genutzt und der von Wang et al. publizierte Algorithmus verwendet.
| Bacteria |
Firmicutes |
Negativicutes |
Selenomonadales |
Veillonellaceae |
Veillonella |
dispar/parvula |
| Bacteria |
Firmicutes |
Bacilli |
Lactobacillales |
Streptococcaceae |
Streptococcus |
australis/cristatus/dentisani/infantis/mitis/oligofermentans/oralis/parasanguinis/peroris/phage/pneumoniae/pseudopneumoniae/rubneri/sanguinis/tigurinus |
| Bacteria |
Actinobacteria |
Actinobacteria |
Micrococcales |
Micrococcaceae |
Rothia |
aeria/dentocariosa |
| Bacteria |
Firmicutes |
Bacilli |
Lactobacillales |
Streptococcaceae |
Streptococcus |
gordonii/mitis/oligofermentans/sanguinis |
| Bacteria |
Firmicutes |
Bacilli |
Lactobacillales |
Carnobacteriaceae |
Granulicatella |
adiacens/para-adiacens |
| Bacteria |
Firmicutes |
Bacilli |
Lactobacillales |
Streptococcaceae |
Streptococcus |
oligofermentans/oralis/parasanguinis/sanguinis |
Hier noch zur Kontrolle die Anzahl nicht klassifizierbarer ASVs in den jeweiligen Gruppen:
Einen phylogenetischen Baum konstruieren
Aus den Sequenzähnlichkeiten lässt sich dann auch noch ein phylogenetischer Baum ableiten, der für einige sich anschließende Analysen notwendig ist. Dazu wurde zunächst ein multiples Alignment mit dem DECIPHER-Paket durchgeführt und anschließend der Baum mit dem phangorn-Paket gebaut.
Alle Daten in ein phyloseq-Objekt kombinieren
Für die sich anschließenden Analysen arbeiten wir mit einem sogenannten “phyloseq”-Objekt. Dieses müssen wir nun nur noch aus den bisher berechneten Teilen zusammenfügen.
Dieses sieht hier wie folgt aus:
## phyloseq-class experiment-level object
## otu_table() OTU Table: [ 1293 taxa and 72 samples ]
## sample_data() Sample Data: [ 72 samples by 7 sample variables ]
## tax_table() Taxonomy Table: [ 1293 taxa by 7 taxonomic ranks ]
## phy_tree() Phylogenetic Tree: [ 1293 tips and 1291 internal nodes ]
Zusammenfassung
Welche Abteilungen wurden gefunden
Insgesamt konnten 17 Abteilungen gefunden werden, von denen 16 zugeordnet werden konnten.
| Firmicutes |
416 |
| Bacteroidetes |
366 |
| Actinobacteria |
160 |
| Proteobacteria |
146 |
| Fusobacteria |
75 |
| Spirochaetae |
74 |
| Saccharibacteria |
22 |
| Synergistetes |
11 |
| Tenericutes |
10 |
| Gracilibacteria |
4 |
Welche Gattungen wurden gefunden
Insgesamt konnten 116 Gattungen gefunden werden.
| Actinomyces |
91 |
| Treponema_2 |
74 |
| Selenomonas_3 |
65 |
| Prevotella |
60 |
| Capnocytophaga |
51 |
| Veillonella |
51 |
| Prevotella_7 |
48 |
| Selenomonas |
43 |
| Leptotrichia |
39 |
Welche Spezies wurden gefunden
Insgesamt konnten 212 Spezies gefunden werden.
| Actinomyces |
odontolyticus |
6 |
| Fusobacterium |
nucleatum |
6 |
| Treponema_2 |
socranskii |
6 |
| Capnocytophaga |
ochracea |
5 |
| Prevotella |
intermedia |
5 |
| Selenomonas |
sputigena |
5 |
| Actinomyces |
naeslundii |
4 |
| Aggregatibacter |
aphrophilus |
4 |
| Treponema_2 |
maltophilum |
4 |
| Actinomyces |
oris/viscosus |
3 |
Wie geht es weiter?
Bis hierher haben wir aus den Rohdaten alle Informationen gewonnen, um alle weiteren Analysen durchführen zu können und die Ergebnisse zu visualisieren. Dies soll Gegenstand eines folgenden Blogeintrages werden.
Außerdem möchte ich darauf hinweisen, dass es mindestens zwei recht einfache Wege gibt, das erzeugte phyloseq-Objekt zu analysieren:
shiny-phyloseq
PathoStat
Beides sind browserbasierte grafische Oberflächen, in denen man ein phyloseq-Objekt laden und analysieren kann. Mittels shiny-phyloseq konnte ich sehr schnell sehen, dass sich das Mikrobiom der Zunge von dem der beiden untersuchten Zahnoberflächen unterscheidet (Abbildung 2 aus Galimanas et al.)
Referenzen
Datenquellen
wissenschaftliche Publikationen
- McMurdie PJ, Holmes S. phyloseq: An R Package for Reproducible Interactive Analysis and Graphics of Microbiome Census Data. PLOS ONE. 2013;8: e61217. doi:10.1371/journal.pone.0061217
- Balvočiūtė M, Huson DH. SILVA, RDP, Greengenes, NCBI and OTT — how do these taxonomies compare? BMC Genomics. 2017;18. doi:10.1186/s12864-017-3501-4
- Callahan BJ, Sankaran K, Fukuyama JA, McMurdie PJ, Holmes SP. Bioconductor Workflow for Microbiome Data Analysis: from raw reads to community analyses. F1000Research. 2016;5: 1492. doi:10.12688/f1000research.8986.2
- Callahan BJ, McMurdie PJ, Rosen MJ, Han AW, Johnson AJA, Holmes SP. DADA2: High-resolution sample inference from Illumina amplicon data. Nature Methods. 2016;13: 581. doi:10.1038/nmeth.3869
- Callahan BJ, McMurdie PJ, Holmes SP. Exact sequence variants should replace operational taxonomic units in marker-gene data analysis. The ISME Journal. 2017;11: 2639. doi:10.1038/ismej.2017.119
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.4.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 17.12.0 (entwickelt von der KDE Community) http://kate-editor.org
- Callahan BJ, McMurdie PJ, Rosen MJ, Han AW, Johnson AJA and Holmes SP (2016). “DADA2: High-resolution sample inference from Illumina amplicon data.” Nature Methods, 13, pp. 581-583. doi: 10.1038/nmeth.3869 (URL: http://doi.org/10.1038/nmeth.3869).
- phyloseq: An R package for reproducible interactive analysis and graphics of microbiome census data. Paul J. McMurdie and Susan Holmes (2013) PLoS ONE 8(4):e61217.
- Wright ES (2016). “Using DECIPHER v2.0 to Analyze Big Biological Sequence Data in R.” The R Journal, 8(1), pp. 352-359.
- Schliep K.P. 2011. phangorn: phylogenetic analysis in R. Bioinformatics, 27(4) 592-593
- Leo Lahti et al. microbiome R package. URL: http://microbiome.github.io
- Hadley Wickham, James Hester and Jeroen Ooms (2017). xml2: Parse XML. R package version 1.1.1. https://CRAN.R-project.org/package=xml2
- Hadley Wickham and Jennifer Bryan (2017). readxl: Read Excel Files. R package version 1.0.0. https://CRAN.R-project.org/package=readxl
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.2.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.8 https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
Kombination von PhenoGraph und t-SNE
Datum: 07.01.2018
Clustering mit dem PhenoGraph Algorithmus
PhenoGraph ist eine Graphen-basierte Methode zur Identifikation von Zellpopulationen in hochdimensionalen Einzelzelldaten. Der Algorithmus repräsentiert die zugrundeliegende Zellpopulationen als Graph (Netzwerk), in dem jede Zelle mit phänotypisch ähnlichen Zellen verbunden ist. Dieser Graph wird anschließend in getrennte phänotypische Gemeinschaften aufgegliedert. PhenoGraph ist leistungsfähig auch für große Proben (>100.000 Zellen), wobei er qualitativ hochwertige Ergebnisse ohne Downsampling ermöglicht. Downsampling ist allerdings notwendig für die Berechnung der t-SNE Karten, sodass ich hier aus 200.000 gemessenen Zellen zufällig 20.000 ausgewählt habe, um beide Methoden zu kombinieren: PhenoGraph zum multidimensionalen Clustering und t-SNE zur zweidimensionalen Darstellung.
t-SNE
Die vom Phenograph-Algorithmus gefundenen Cluster wollen wir nun wieder als XY-Plot darstellen. Dafür berechnen wir zunächst die t-SNE-Karte und färben jede Zelle entsprechend ihrer Cluster-Zugehörigkeit.
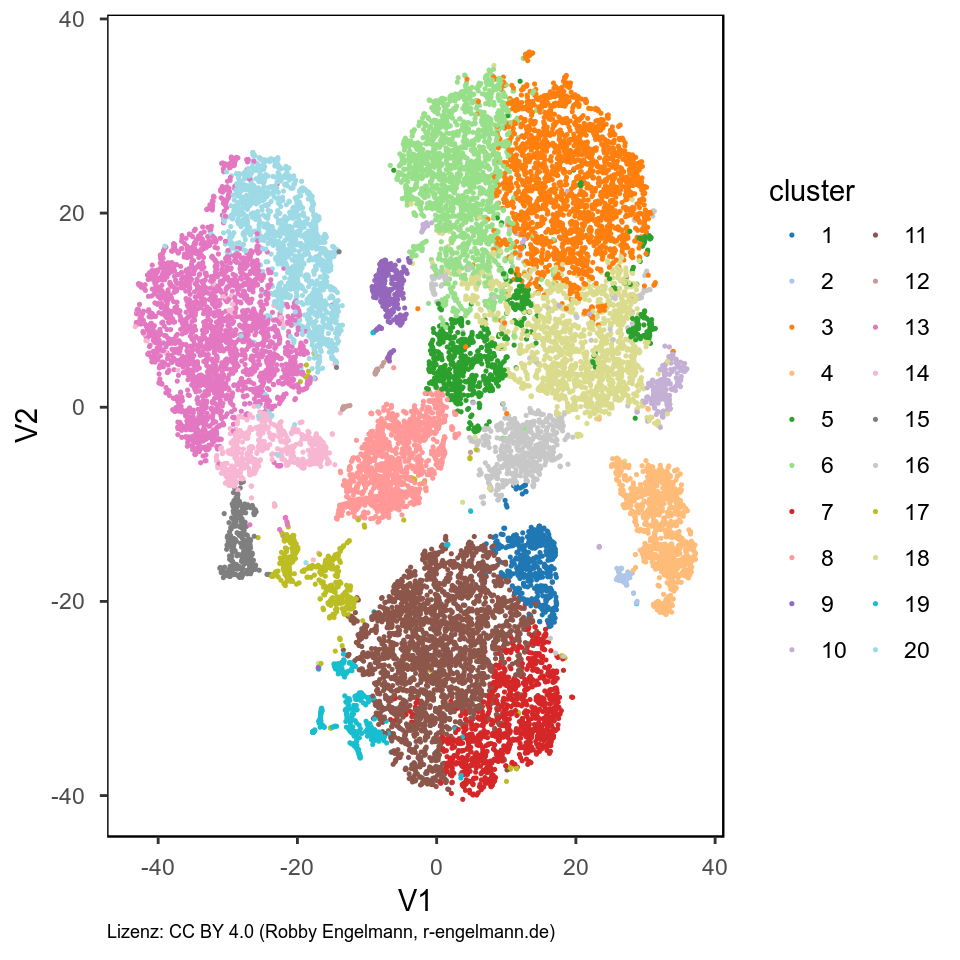
Analyse der gefundenen Populationen
Anschließend können wir uns die gefundenen Zellpopulationen (=Cluster) genauer untersuchen.
1. Größe der gefundenen Populationen
Als erstes interessiert mich die Anzahl der Zellen, die sich in jedem Cluster befindet. Also ob es sich um ein großes oder kleines Cluster handelt. Hier bietet sich ein Kreisdiagramm an.
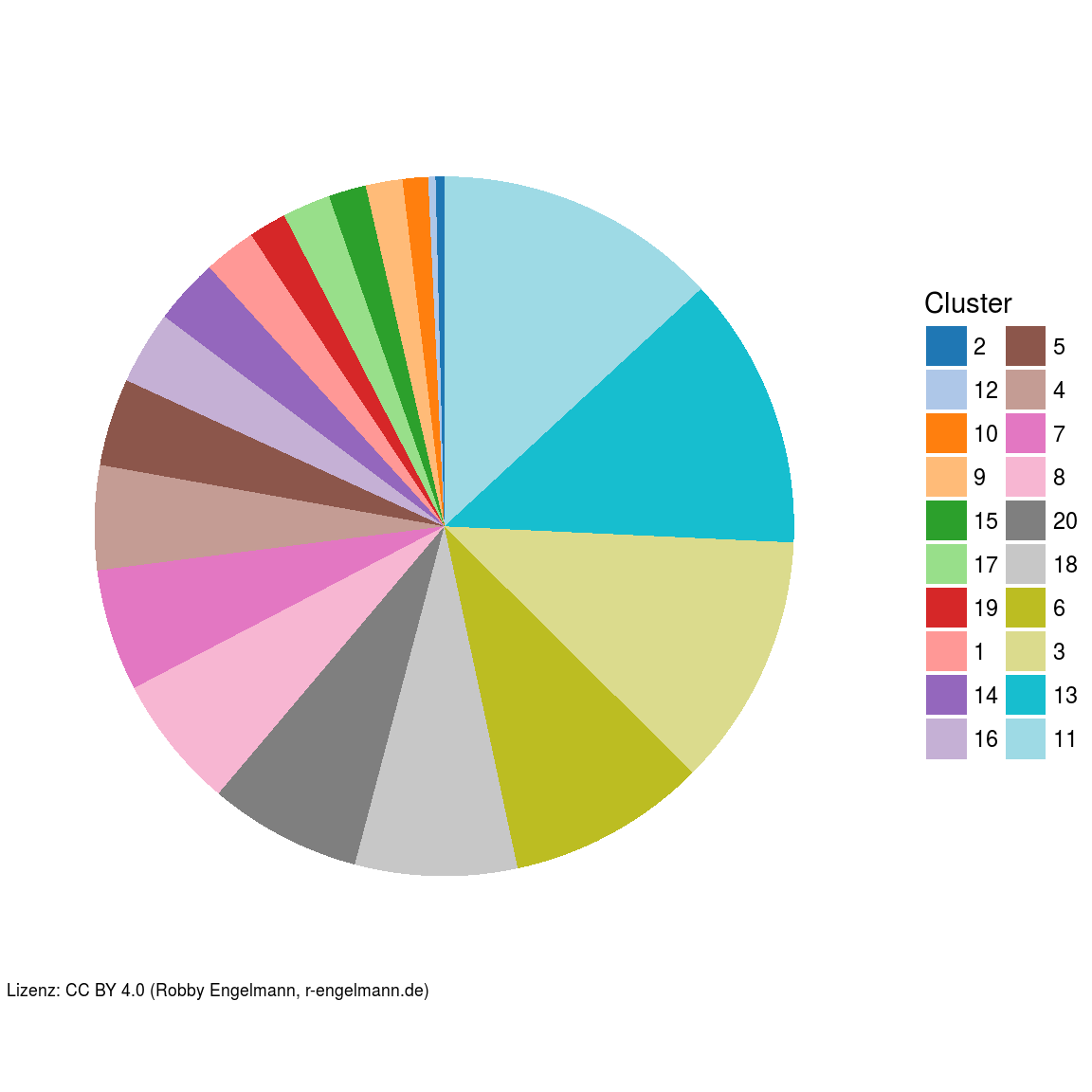
Dieses Kreisdiagramm wirkt mit seinen 20 Sektoren sehr unübersichtlich. Daher bietet sich zur Visualisierung der Anteile der einzelnen Cluster folgende Alternative an.
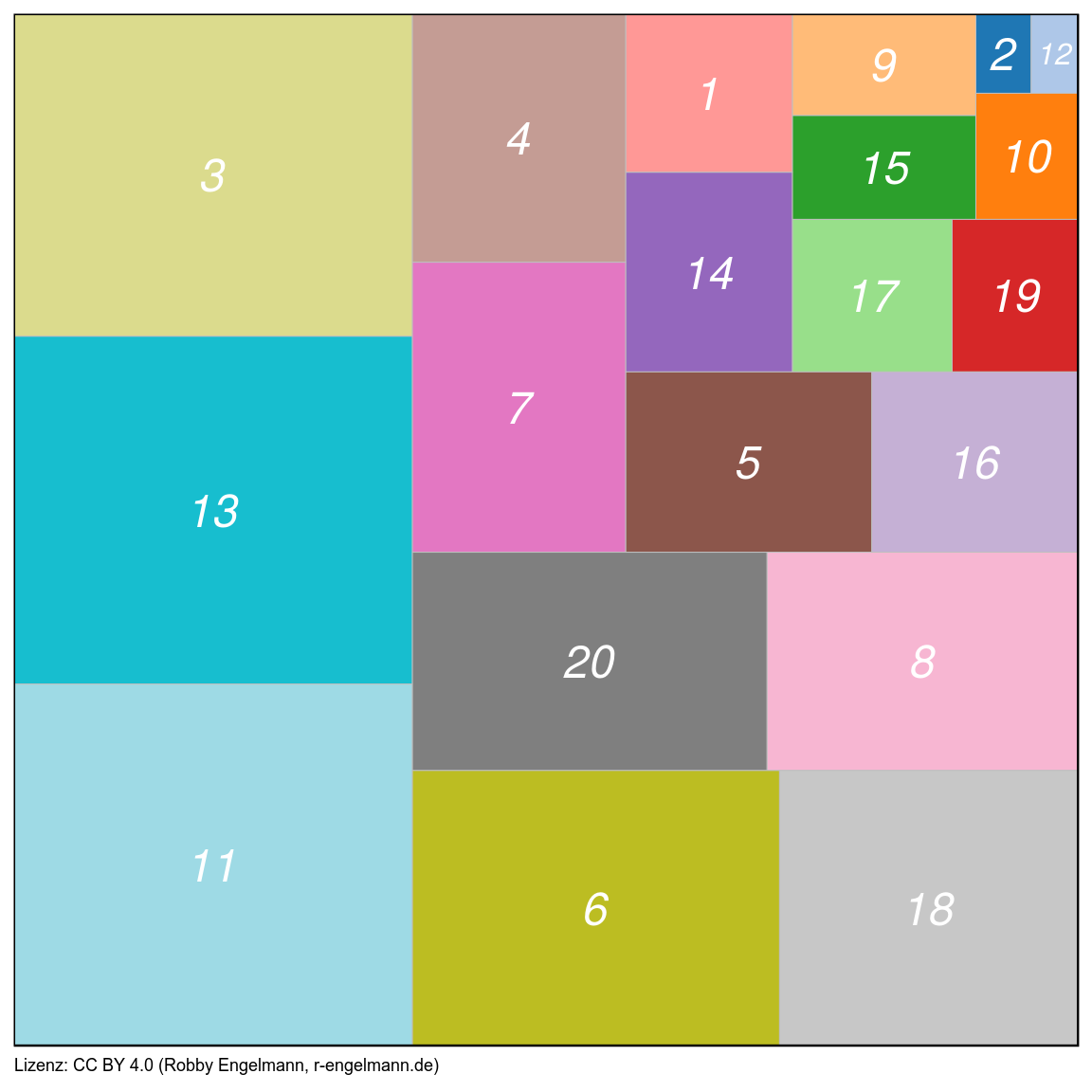
2. t-SNE-Karte mit Markerexpression
Außerdem lässt sich die Expression der verschiedenen Marker direkt in der t-SNE-Karte zeigen. Dies veranschaulicht die folgende Grafik.
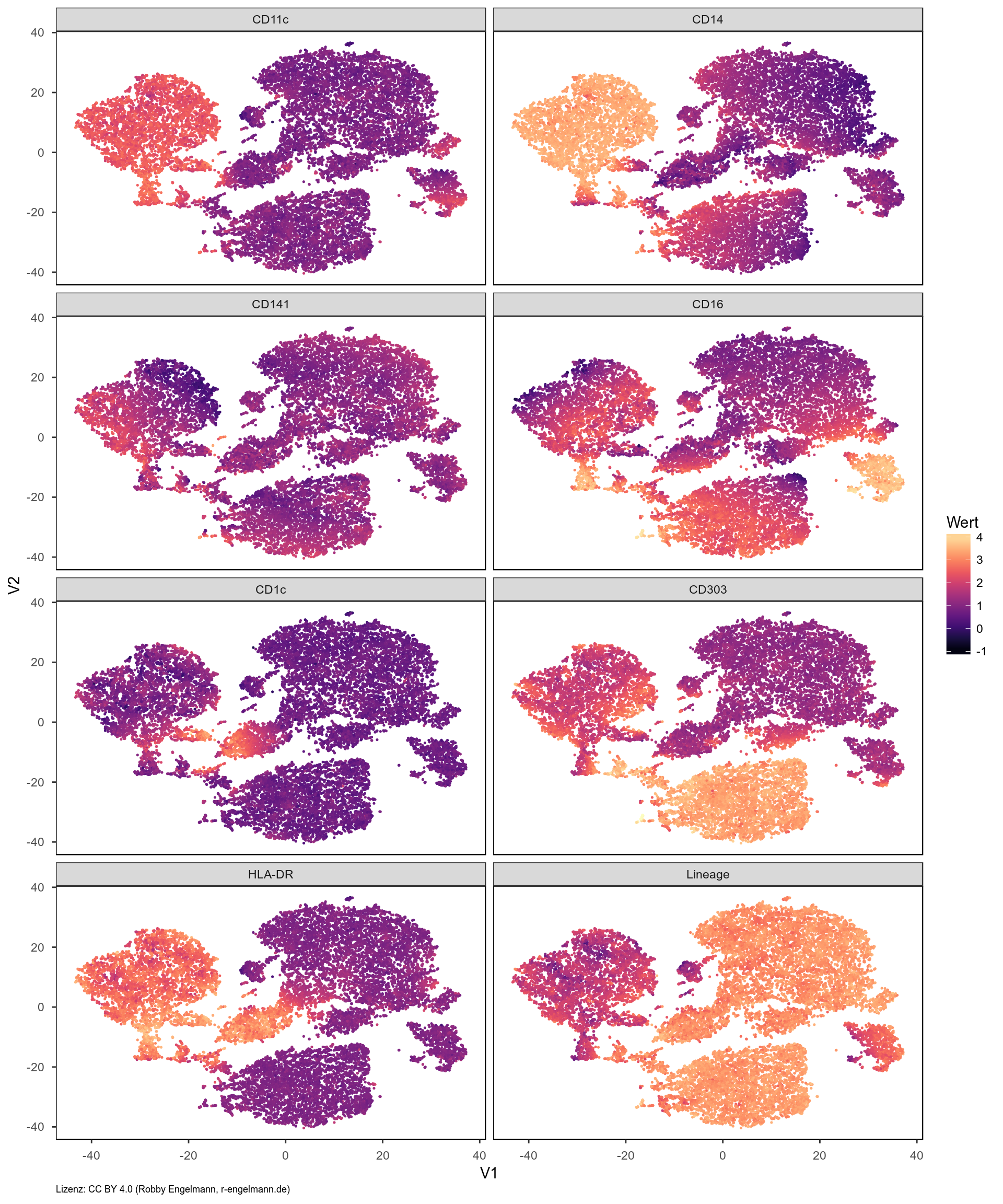
3. Mittlere Markerexpression der gefundenen Zellpopulationen
Des Weiteren können wir uns die mittlere Expression der gemessenen Marker auf den gefundenen Zellpopulationen auch als Heatmap anzeigen lassen.
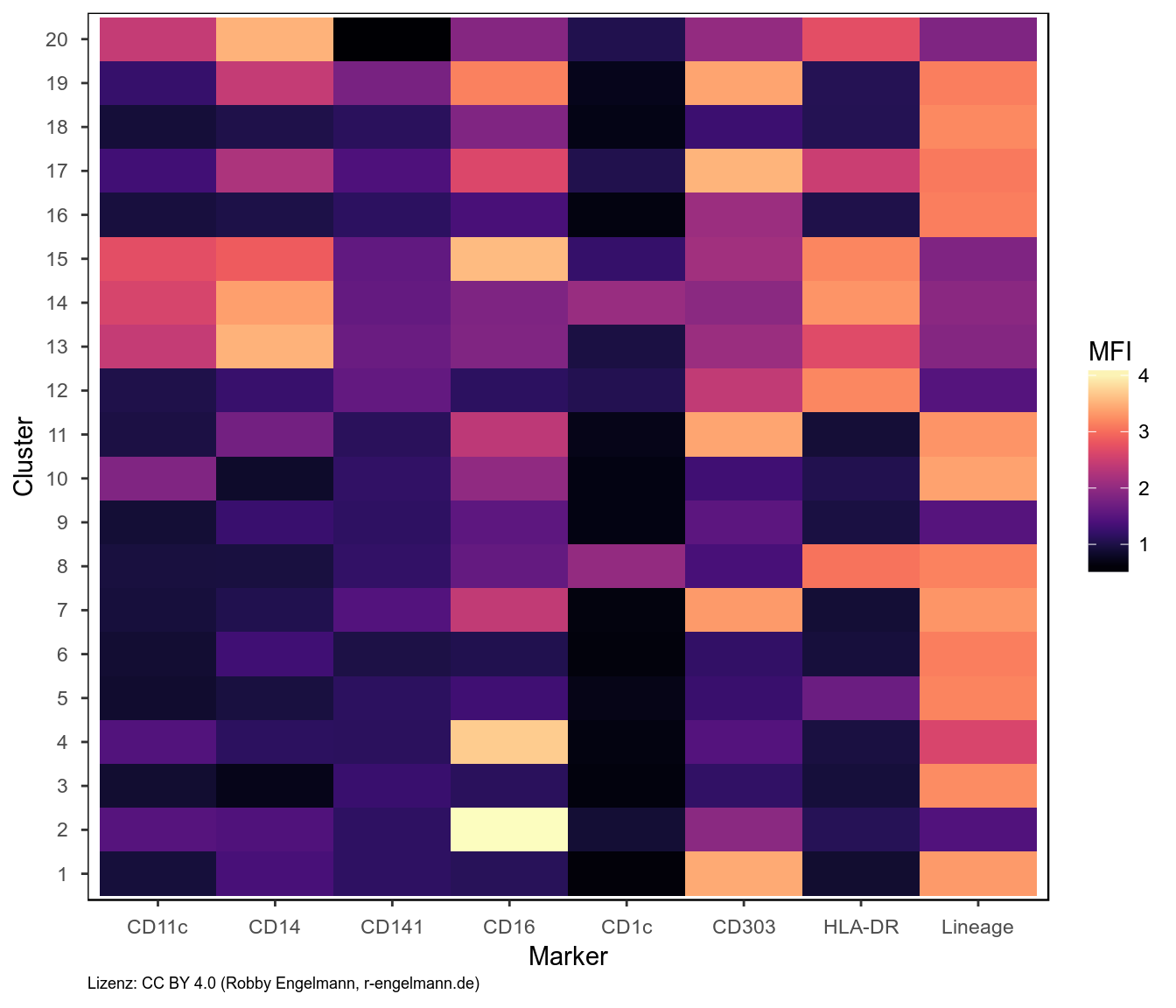
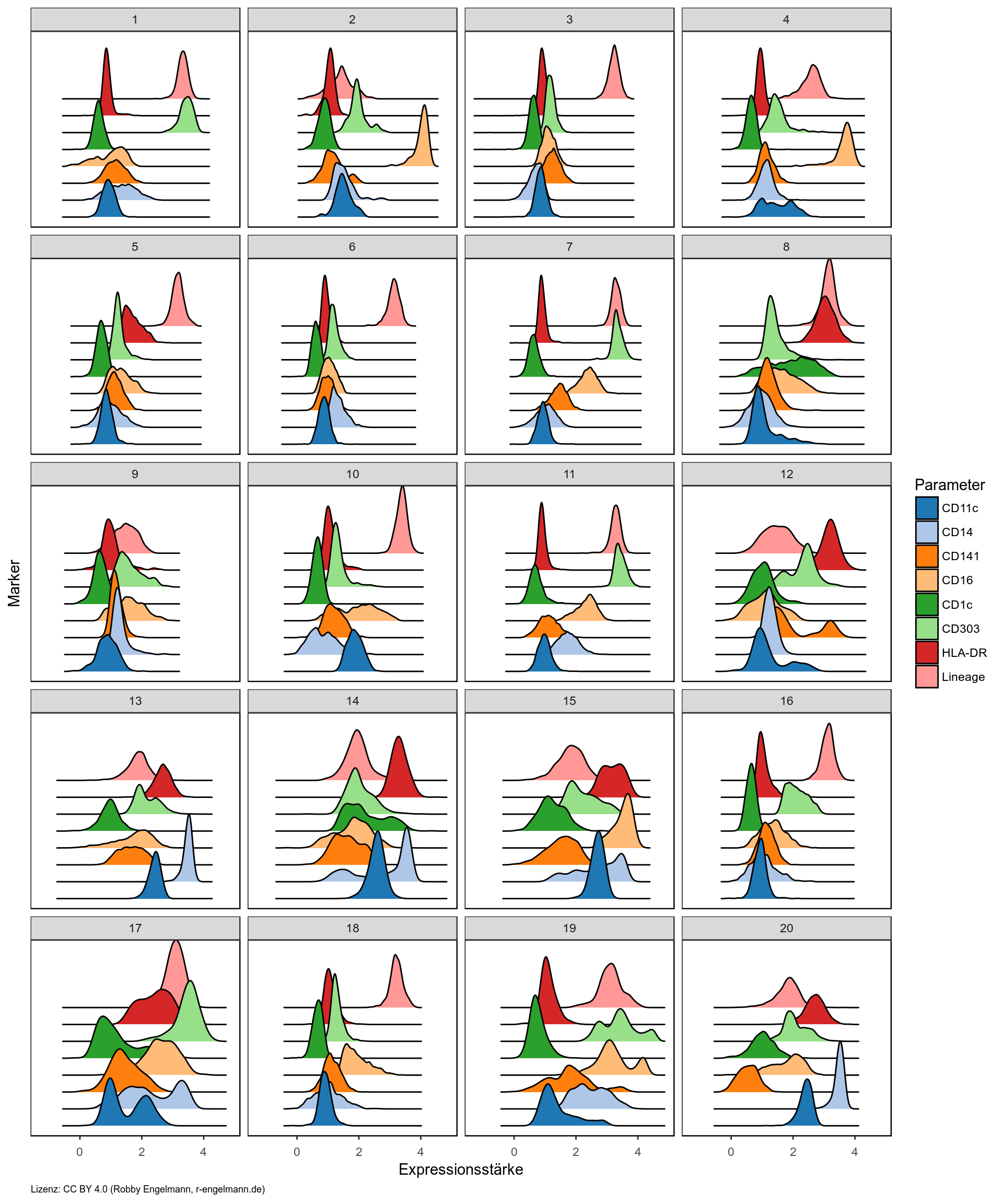
4. Histogramme der Markerexpression der gefundenen Zellpopulationen
Die Heatmap zeigt jedoch nur die mittlere Expression. Möchte man sich die Expression der unterschiedlichen Marker genauer anschauen, so kann man sich diese auch als Histogramme anzeigen lassen. In der folgenden Grafik habe ich dazu den sogenannten Ridgeline-Plot verwendet. Die Zahl im Titelfeld jeder Untergrafik gibt dabei das jeweilige Cluster an.
Trotz Nutzung der aktuellsten Algorithmen dauert diese Art der Analyse sehr lang. Auf meinem Tuxedo Infinity Book v2 benötigte der komplette Durchlauf des R-Codes für diesen Blogeintrag ca. 10 Minuten. Den längsten Anteil (fast 9 Minuten) hatte dabei die Berechnung der t-SNE-Karte, während der Phenograph-Algorithmus lediglich 30-40 Sekunden läuft.
Referenzen
Datenquellen
Beispiel FCS-File aus einer bereits publizierten Studie.
wissenschaftliche Publikationen
- Levine JH, Simonds EF, Bendall SC, Davis KL, Amir ED, Tadmor MD, Litvin O, Fienberg HG, Jager A, Zunder ER, Finck R, Gedman AL, Radtke I, Downing JR, Pe’er D, Nolan GP. Data-Driven Phenotypic Dissection of AML Reveals Progenitor-like Cells that Correlate with Prognosis, Cell 2015
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.4.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 17.12.0 (entwickelt von der KDE Community) http://kate-editor.org
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.2.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Claus O. Wilke (2017). ggridges: Ridgeline Plots in ‘ggplot2’. R package version 0.4.1. https://CRAN.R-project.org/package=ggridges
- David Wilkins (2017). treemapify: Draw Treemaps in ‘ggplot2’. R package version 2.4.0. https://CRAN.R-project.org/package=treemapify
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- Simon Garnier (2017). viridis: Default Color Maps from ‘matplotlib’. R package version 0.4.0. https://CRAN.R-project.org/package=viridis
- Greg Finak and Mike Jiang (2011). flowWorkspace: Infrastructure for representing and interacting with the gated cytometry. R package version 3.26.3
- Sofie Van Gassen, Britt Callebaut and Yvan Saeys (2017). FlowSOM:Using self-organizing maps for visualization and interpretation of cytometry data. http://www.r-project.org, http://dambi.ugent.be.
- Finak G., Frelinger J., Newell E.W., Ramey J., Davis M.M., Kalams S.A., De Rosa S.C., Gottardo R. (2014) OpenCyto: An Open Source Infrastructure for Scalable, Robust, Reproducible, and Automated, End-to-End Flow Cytometry Data Analysis. PLoS Comput Biol 10:e1003806.
- L.J.P. van der Maaten. Accelerating t-SNE using Tree-Based Algorithms. Journal of Machine Learning Research 15(Oct):3221-3245, 2014.
- Jesse H. Krijthe (2015). Rtsne: T-Distributed Stochastic Neighbor Embedding using a Barnes-Hut Implementation, URL: https://github.com/jkrijthe/Rtsne
- Chen H, Lau MC, Wong MT, Newell EW, Poidinger M, et al. (2016): Cytofkit: A Bioconductor Package for an Integrated Mass Cytometry Data Analysis Pipeline. PLoS Comput Biol 12(9): e1005112. doi: 10.1371/journal.pcbi.1005112
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.8 https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
Dimensionsreduktion und Clustering am Beispiel von Durchflusszytometriedaten
Datum: 07.09.2017
Durchflusszytometriedaten
Die Durchflusszytometrie wird in der biomedizinischen Forschung häufig zur Identifikation von Zelltypen anhand der Proteinexpression bekannter Marker auf der Zelloberfläche oder dem Zellinneren genutzt. Im hier vorgestellten Beispiel ist eine Kombination aus acht solchen Markern verwendet worden, um bestimmte Typen von Immunzellen zu bestimmen. Nach heutigem Stand der Technik ist es bereits möglich bis zu 28 solcher Marker parallel zu messen. In Zukunft werden es wohl an die 50 sein. Plant man ein solches Experiment, hat man vorher zumeist eine Vorstellung, welche Marker für welche Zellpopulationen gemessen werden sollen. Aufgrund der Kombinatorik einer solch großen Anzahl an Markern besteht allerdings die Gefahr, dass man z.B. bisher unbekannte Zelltypen übersieht, die funktionell und ontogenetisch durch eine bestimmte Markerkombination charakterisiert sind. Um dem zu entgehen gibt einige Methoden, die eine unvoreingenomme Sicht auf die Daten erlauben.
Dimensionsreduktion
Der Mensch ist nicht dafür gemacht sich mehr als 3 Dimensionen vorstellen zu können. Bei der Datenanalyse betrachtet man zumeist immer nur zwei Parameter zugleich, einer auf der x-Achse und einer auf der y-Achse eines Diagramms. Sind in einem Datensatz allerdings deutlich mehr Messparameter zu untersuchen, so bietet es sich an, Algorithmen zur Dimensionsreduktion anzuwenden. Diese versuchen mit möglichst wenig Informationsverlust den Datensatz auf zwei Dimensionen zu projizieren.
Hauptkomponentenanalyse
Ein solcher Algorithmus ist die Hauptkomponentenanalyse (engl.: Principal Component Analysis, PCA). Dabei werden potentiell miteinander korrelierte Parameter durch bestimmte Transformationen in linear unkorrelierte sog. Hauptkomponenten überführt. Von diesen Hauptkomponenten vereinigt die Erste die höchste Varianz und die zweite Hauptkomponente die zweithöchste Varianz der ursprünglichen Daten. Diese beiden Hauptkomponenten spiegeln damit den überwiegenden Teil der ursprünglich in den Daten enthaltenen Information wider und werden typischerweise gegeneinander dargestellt.
Im folgenden Beispiel wurden die beiden ersten Hauptkomponenten aus unseren Durchflusszytometriedaten als Punktediagramm inklusive Dichtelinien dargstellt. In der Grafik kann man 7-10 mehr oder weniger deutlich voneinander abgrenzbare Datenbereiche erkennen. Jeder dieser Datenbereiche könnte einem Zelltyp entsprechen.
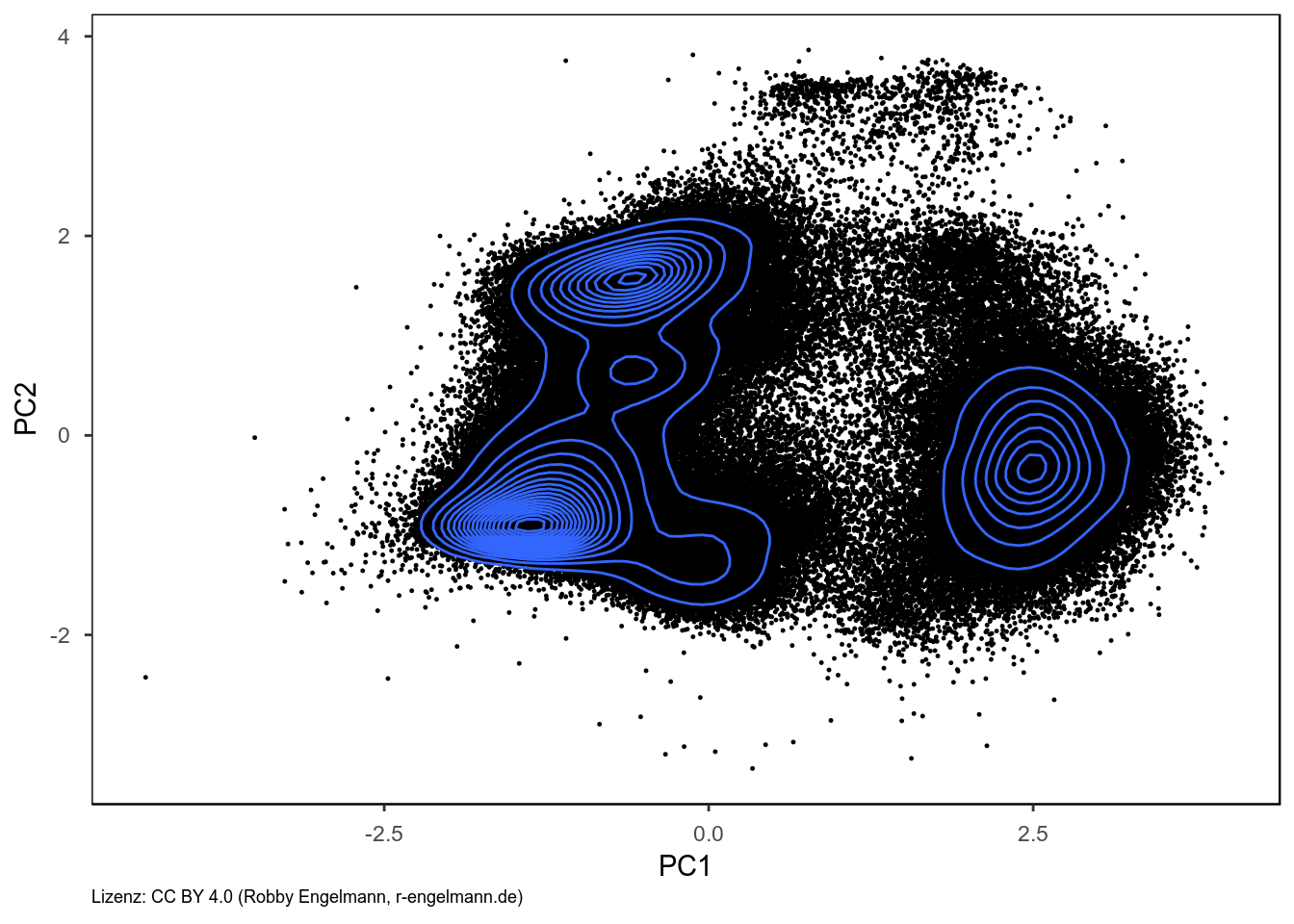
t-SNE
Ein etwas neuerer Algorithmus nennt sich t-SNE (t-distributed stochastic neighbor embedding) und wird auch bereits von bekannter Auswertesoftware für Durchflusszytometriedaten angeboten. In dem entsprechenden Punktediagramm, das aus den selben Daten wie bei der PCA berechnet wurde, erkennt man mehr voneinander getrennte Datenbereiche (10-12). Außerdem sind Bereiche zu sehen, in denen nur wenige Datenpunkte liegen, die aber dennoch deutlich von anderen Bereichen getrennt sind. Diese Methode der Dimensionsreduktion eignet sich potentiell besser für Durchflusszytometriedaten, da auch weniger häufig vertretene Zelltypen visualisiert werden können.
Die Methode hat aber auch einige Nachteile. So ist man bei Datensätzen mit vielen Beobachtungen gezwungen, sich auf eine Auswahl zu beschränken, da sonst die Berechnung sehr lange dauern kann. Im Beispiel hier lief der Algorithmus auf einer zufälligen Auswahl von 20.000 Datenpunkten aus einer Gesamtheit von 250.000 Datenpunkten und benötigte trotzdem wesentlich mehr Zeit als die Berechnung der PCA auf dem vollständigen Datensatz. Außerdem arbeitet der Algorithmus nicht-deterministisch, die Zellpopulationen in einer gemessenen Proben liegen im Punktediagramm nicht zwingenderweise an der jeweils gleichen Stellen, wenn man Daten einer anderen Probe mit den gleichen Zellpopulationen analysiert.
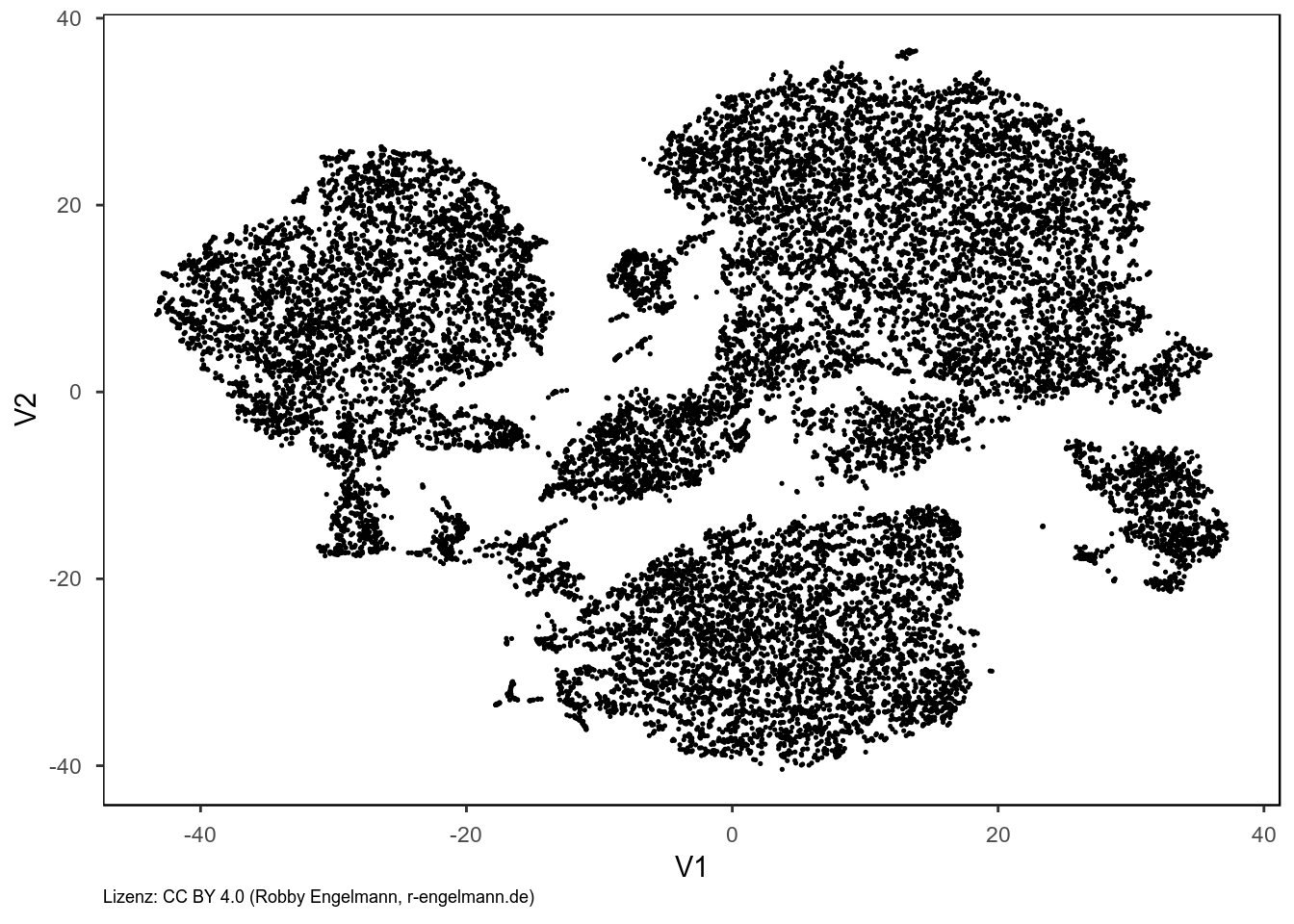
Clustering
Clustering bezeichnet Verfahren zur Erkennung von gleichartigen oder auch zusammengehörigen Datenpunkten in einem Datensatz. Hier wollen wir eine Auswahl verschiedener Clusterverfahren testen, um möglichst automatisch die einzelnen einheitlichen Datenbereiche zu erkennen und den einzelnen Beobachtungen zuzuordnen.
k-Means Clustering
Eine einfach und schnelle Form ist das k-Means Clustering. Dem Algorithmus übergibt man die Anzahl an Bereichen, in denen die Daten unterteilt werden sollen. Dann sucht der Algorithmus die Zentren der Cluster wobei er Gruppen mit geringer Varianz und ähnlicher Größe bevorzugt. Im Beispiel hier, habe ich die Daten in 10 Bereiche geteilt. Man kann sehen, dass die Unterteilung kaum optimal ist, da die großen Bereich scheinbar willkürlich zerteilt werden und z.T. weit getrennte Bereiche einem Cluster zugeordnet werden.
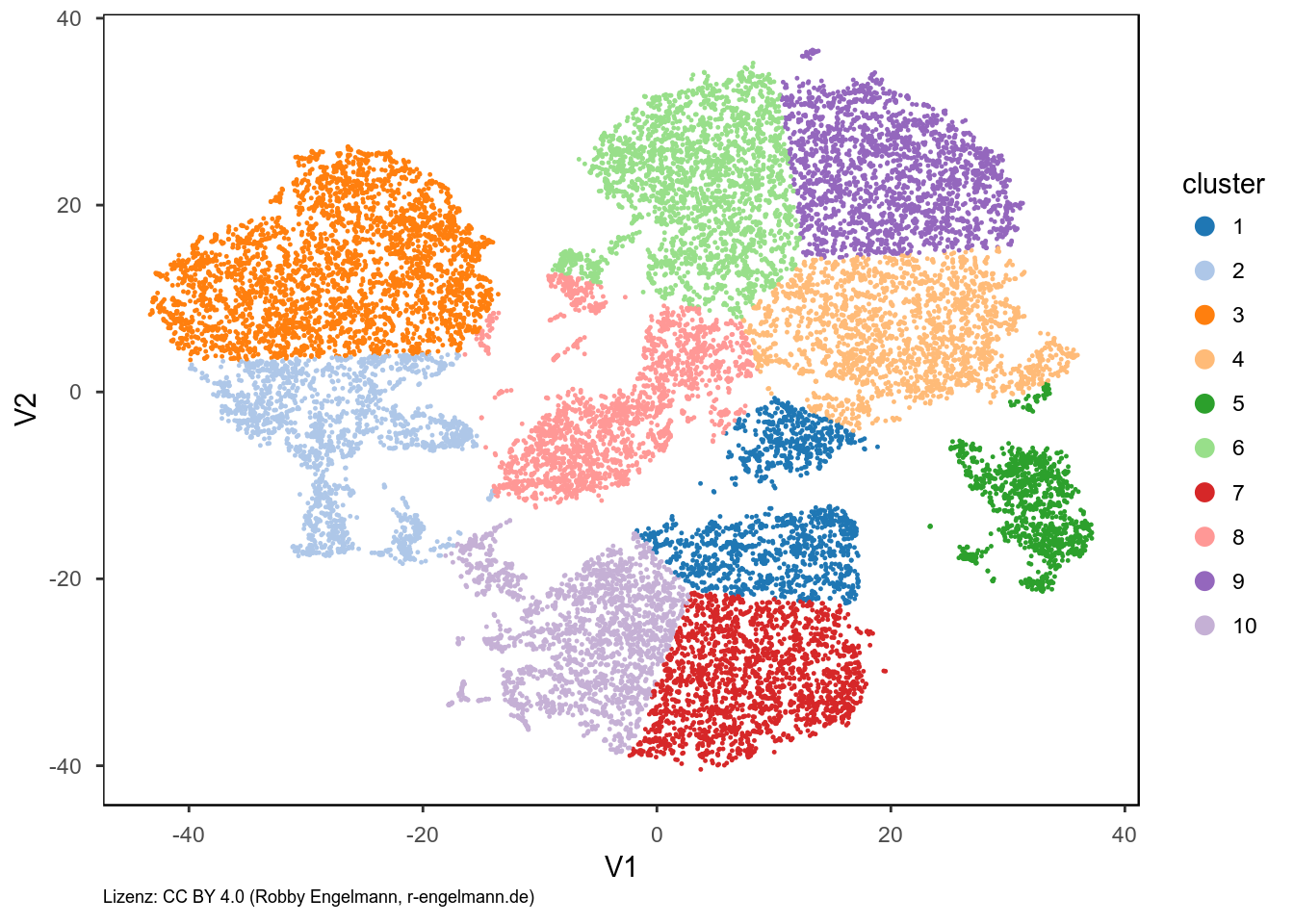
Spektrales Clustering
Die Algorithmen für das spektrale Clustering basieren letzlich auf Graphen, die zu clusternden Objekte sind die Knoten und werden mit gewichteten Kanten verbunden. Die Kanten werden dann entsprechend bestimmter Regeln nach und nach entfernt. Das spektrale Clustering scheint in unserem Beispiel etwas besser zu funktionieren, doch auch hier wird z.b. der mittlere untere Bereich zerteilt (grün/orange).
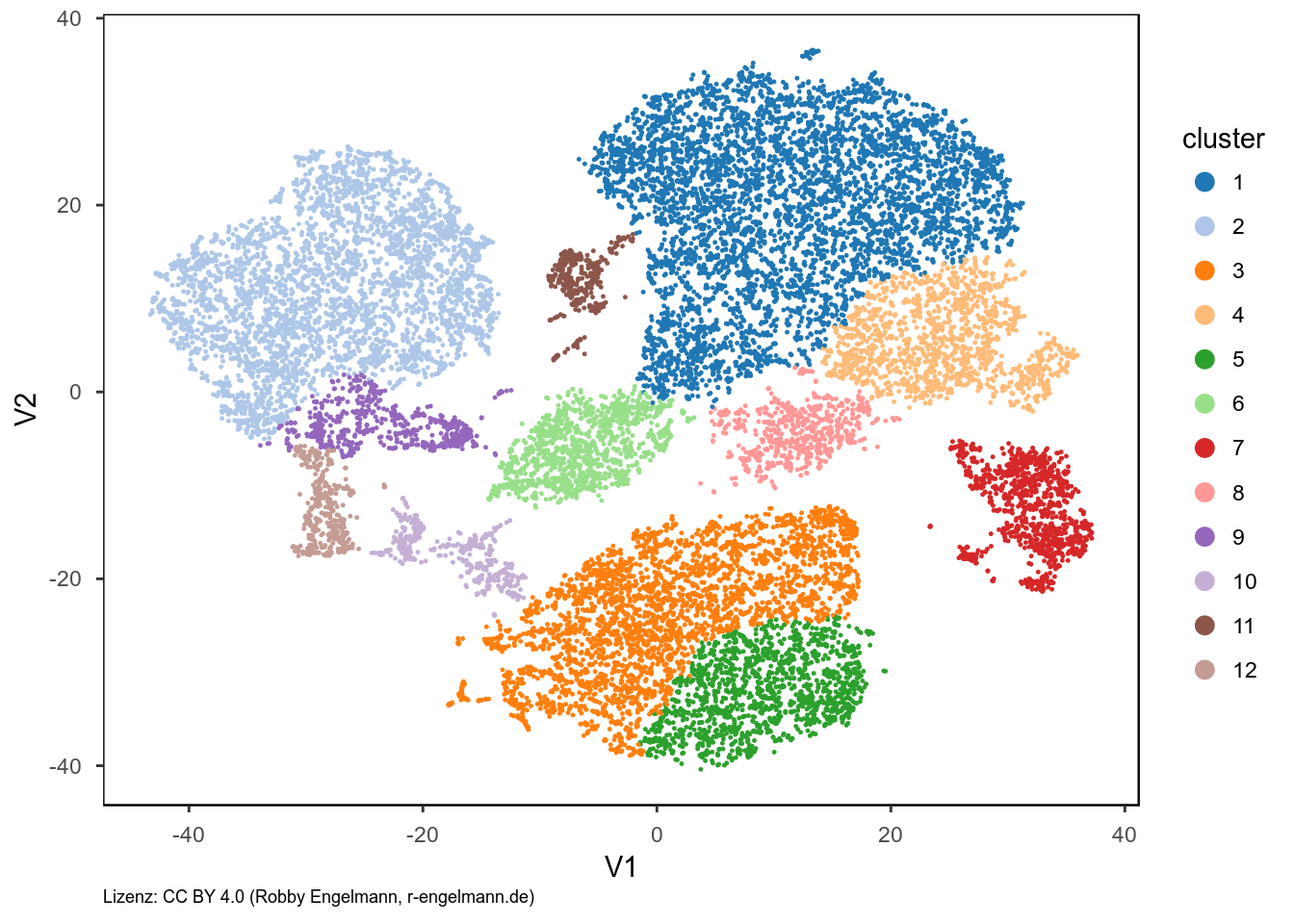
Hierarchisches Clustering
Das hierarchische Clustering ist eine Gruppe von distanzbasierten Gruppierungsalgorithmen. Die Objekte eines Clusters haben eine geringere Distanz zueinander als zu Objekten eines anderen Clusters. Dabei kann man das Distanzmaß frei wählen. Hier wurde mit der euklidischen Distanz als Abstandsmaß gearbeitet und der entstehende Hierarchiebaum so geteilt, dass zehn Cluster mit größter Distanz zueinander entstehen.
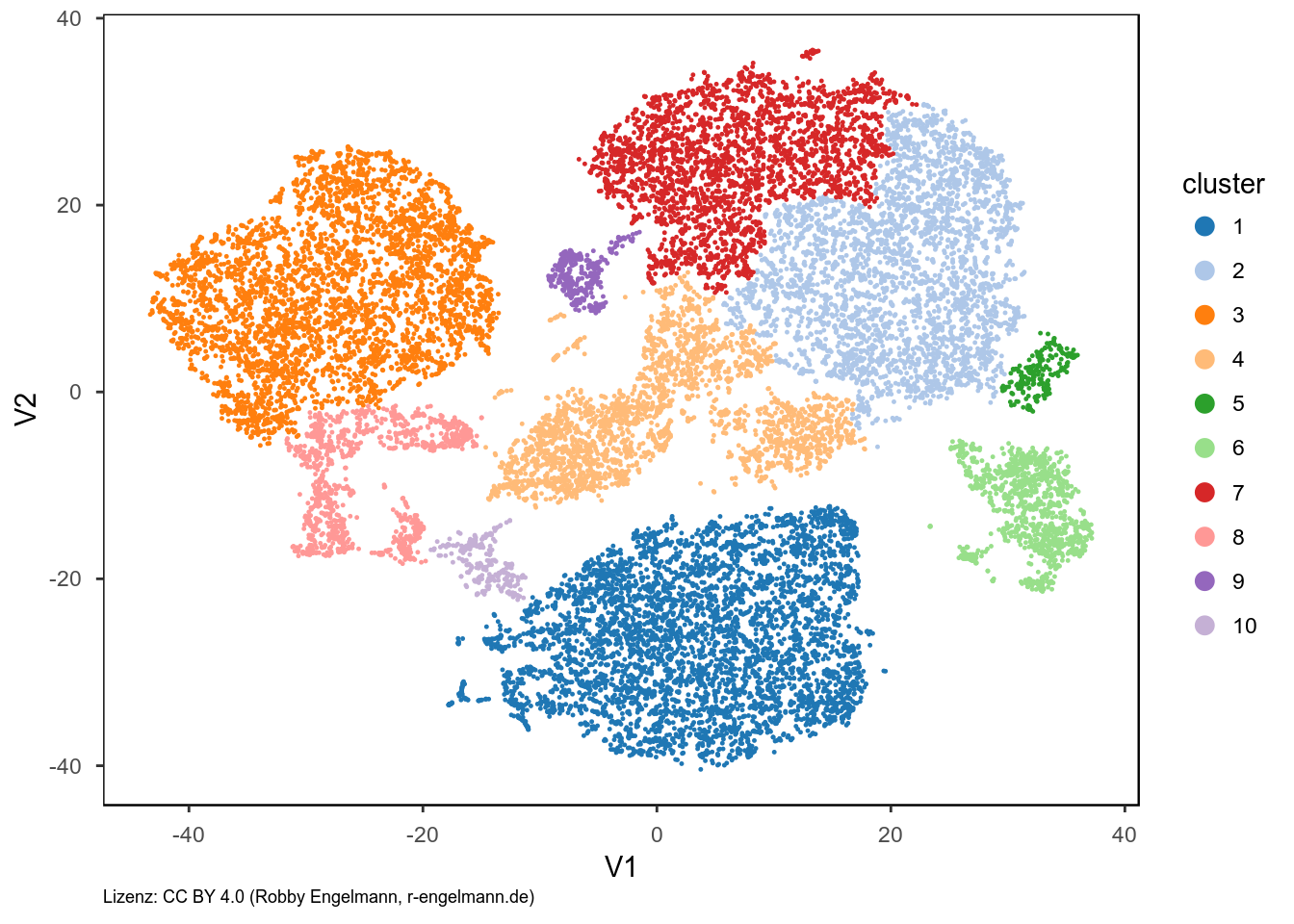
Analyse der gefundenen Populationen
Anschließend können wir uns die gefundenen Zellpopulationen (=Cluster) genauer anschauen und deren jeweilige Expression der untersuchten Marker z.B. als Heatmap visualisieren.
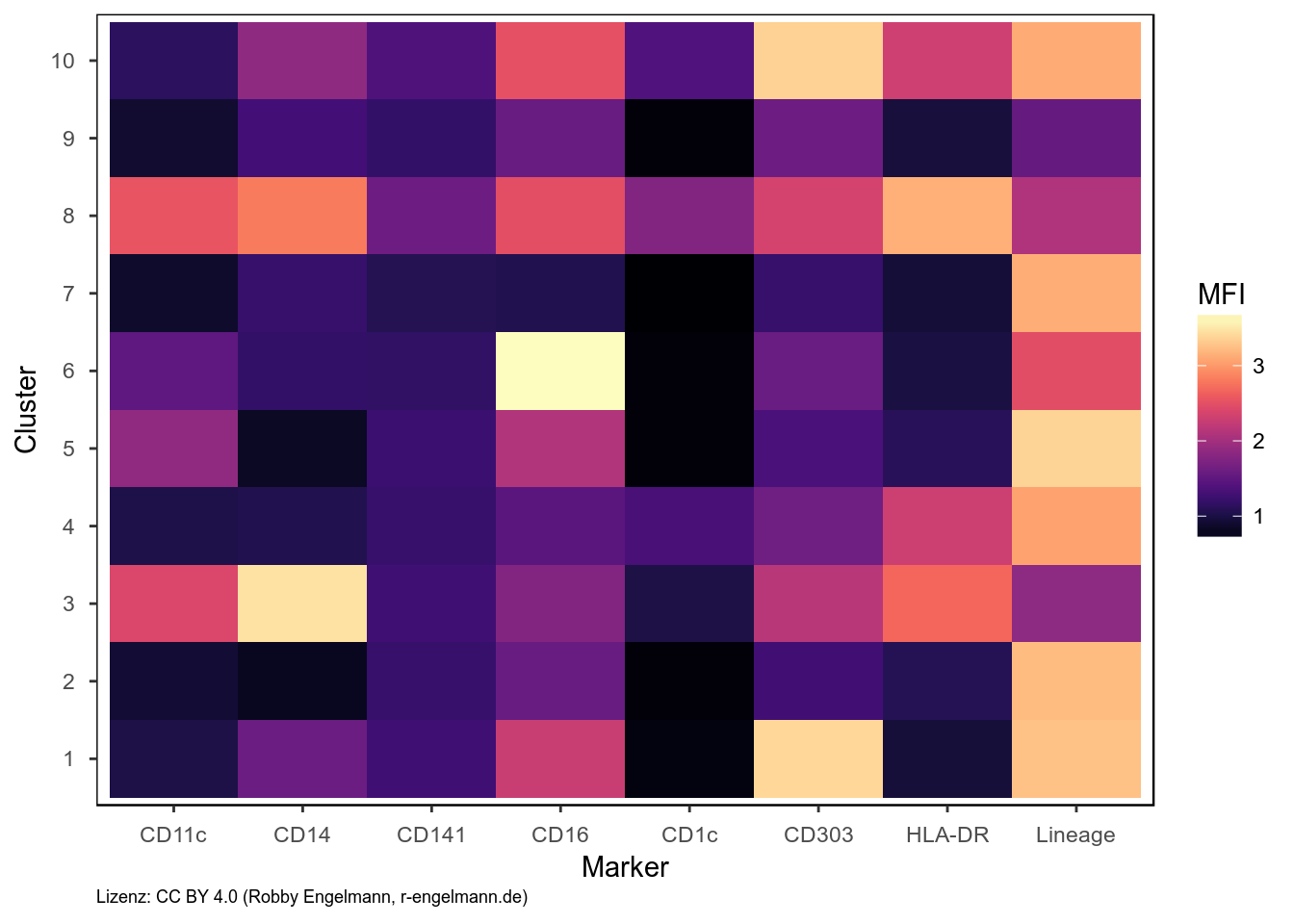
FlowSOM
Bisher haben unsere Clusteralgorithmen “nur” auf den zwei-dimensionalen Daten des t-SNE gearbeitet. Die Gruppeneinteilung kann man aber natürlich auch anhand aller vorhandenen Parameter vornehmen lassen. Nur zur zweidimensionalen Visualisierung der gefundenen Gruppen wird dann anschließend die Dimensionsreduktion, z.B. via t-SNE, vorgenommen.
Ich möchte in diesem Abschnitt daher FlowSOM vorstellen. Dies ist ein neuerer Algorithmus, der auf der Gesamtheit der Daten arbeitet und speziell für Durchflusszytometriedaten entwickelt wurde. Er liefert ähnliche Ergebnisse, wie der populär gewordene SPADE-Algorithmus, doch die Laufzeit verlängert sich mit steigender Anzahl der gemessenen Zellen nicht wesentlich.

Auch mittels FlowSOM läßt sich die Anzahl der Cluster festlegen und den Datenpunkten im t-SNE Plot zuordnen:

Referenzen
Datenquellen
Beispiel FCS-File aus einer bereits publizierten Studie.
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.4.0 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 17.04.1 (entwickelt von der KDE Community) http://kate-editor.org
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- Simon Garnier (2017). viridis: Default Color Maps from ‘matplotlib’. R package version 0.4.0. https://CRAN.R-project.org/package=viridis
- Greg Finak and Mike Jiang (2011). flowWorkspace: Infrastructure for representing and interacting with the gated cytometry. R package version 3.24.4.
- Sofie Van Gassen, Britt Callebaut and Yvan Saeys (2017). FlowSOM:Using self-organizing maps for visualization and interpretation of cytometry data. http://www.r-project.org, http://dambi.ugent.be.
- Finak G., Frelinger J., Newell E.W., Ramey J., Davis M.M., Kalams S.A., De Rosa S.C., Gottardo R. (2014) OpenCyto: An Open Source Infrastructure for Scalable, Robust, Reproducible, and Automated, End-to-End Flow Cytometry Data Analysis. PLoS Comput Biol 10:e1003806.
- L.J.P. van der Maaten. Accelerating t-SNE using Tree-Based Algorithms. Journal of Machine Learning Research 15(Oct):3221-3245, 2014.
- Jesse H. Krijthe (2015). Rtsne: T-Distributed Stochastic Neighbor Embedding using a Barnes-Hut Implementation, URL: https://github.com/jkrijthe/Rtsne
- Zare, H, et al.(2010) Data Reduction for Spectral Clustering to Analyse High Throughput Flow Cytometry Data, BCM Bioinformatics.URL: http://www.biomedcentral.com/1471-2105/11/403/.
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.4 https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
Textanalyse - Wahlprogramme der Parteien zur Bundestagswahl
Datum: 12.08.2017
Übersicht
Heute möchte ich eine einfache Textanalyse am Beisiel der Wahlprogramme der größeren Parteien zur Bundestagswahl 2017 demonstrieren. Die Wahlprogramme habe ich mir von den Webauftritten der Parteien als pdf heruntergeladen.
Die Texte aus den pdf-Dateien habe ich zunächst eingelesen und vorverarbeitet. Die typischen Schritte sind dabei: 1. Auswahl auf die Wörter eingrenzen (Zahlen, Sonderzeichen, Zeichensetzungen werden dabei vor der Analyse entfernt) 2. alle Wörter kleingeschrieben (tolowercase) 3. Stopwörter (Wörter ohne bzw. mit wenig Informationsgehalt, z.B. “und”, “sowie” oder “daher”) entfernen.
Nach diesen Schritten wollte ich die Auswahl auf die Wörter mit dem höchsten Informationsgehalt eingrenzen. Zunächst habe ich die Auswahl auf die Wörter mit vier und mehr Buchstaben eingeschränkt. Außerdem habe ich bestimmte Wörter, die u.a. in Fuß- oder Kopfzeilen und damit häufig vorkommen aber nicht zum Haupttext gehören, aus der Analyse ausgeschlossen. Folgende Wörter sind so aus der Analyse ausgeschlossen: “bundestagswahl”, “wahlprogramm”, “bundestagswahlprogramm”. Durch die Einschränkung auf vier und mehr Buchstaben sind einige sicher interessante Wörter nicht mehr in der Analyse enthalten. Daher wurden folgende Wörter trotzdem berücksichtigt: eu, fdp, afd, cdu, csu und spd.
Die Ergebnisse der Analysen werden auch im Folgenden nicht kommentiert, sondern nur grafisch dargestellt und die Methodik beschrieben.
Zum Überblick zunächst die Anzahl der Wörter, die je Partei für die Analyse verwendet wurde.
| SPD |
17964 |
| CDU+CSU |
9600 |
| Die LINKE |
30775 |
| Grüne |
31537 |
| FDP |
18151 |
| AfD |
9242 |
| Freie Wähler |
10706 |
Über alle Wahlprogramme hinweg sind die Wörter “wollen”, “Menschen” und “Deutschland” am häufigsten vertreten. Dargestellt werden kann die Worthäufigkeit z.B. als Balkendiagramm oder als Wordcloud.

Welches sind die häufigsten Wörter?
Als nächstes wollte ich wissen, welches die am häufigsten vertretenen Wörter in den Wahlprogrammen der einzelnen Parteien sind.

Durch welche Wörter unterscheiden sich die Parteiprogramme?
Weiterhin interessierte mich, welche Wörter die Wahlprogramme der einzelnen Parteien am stärksten von allen anderen Parteien abgrenzen.

Sentimentanalyse
Für die Sentimentanalyse werden die Wörter der einzelnen Wahlprogramme verglichen mit einer Wortliste, die einzelnen Worten eine positive, negative oder neutrale Assoziation zuweist. In den Wahlprogrammen aller Parteien überwiegen die Wörter mit positiver Assoziation deutlich. Es gibt nur geringe Unterschiede zwischen den Parteien.

Emotionen
Für die Zuordnung von Emotionen geht man analog zum Sentiment vor. Hier braucht man zunächst eine Wortliste, die einzelnen Wörtern ein Gefühl zuordnet. Wenn man sich diese Wortlisten anschaut, kann man sich über einzelne Zuordnungen sicher streiten. Außerdem sind entsprechende Assoziationen natürlich auch immer vom jeweiligen Kontext abhängig. Daher ist die Aussagekraft dieser Analysen oft streitbar.

Referenzen
Datenquellen
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.4.1 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 17.04.2 (entwickelt von der KDE Community) http://kate-editor.org
- Jeroen Ooms (2017). pdftools: Text Extraction, Rendering and Converting of PDF Documents. R package version 1.3. https://CRAN.R-project.org/package=pdftools
- Silge J and Robinson D (2016). “tidytext: Text Mining and Analysis Using Tidy Data Principles in R.” JOSS, 1(3). doi:10.21105/joss.00037.
- Hadley Wickham (2017). stringr: Simple, Consistent Wrappers for Common String Operations. R package version 1.2.0. https://CRAN.R-project.org/package=stringr
- Ian Fellows (2014). wordcloud: Word Clouds. R package version 2.5. https://CRAN.R-project.org/package=wordcloud
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Hadley Wickham (2016). scales: Scale Functions for Visualization. R package version 0.4.1. https://CRAN.R-project.org/package=scales
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins, Rob Hyndman and Ruben Arslan (2017). rmarkdown: Dynamic Documents for R. R package version 1.6. https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
RDI- und Horizontplot
Datum: 21.05.2017
RDI Plot
In meinem Blogeintrag zur Visualisierung von Gruppendaten bin ich bereits auf die verschiedenen Darstellungsformen beginnend beim Balkendiagramm eingegangen und habe gezeigt, dass das Balkendiagramm den geringen Informationsgehalt bietet und in Abhängigkeit von der Verteilung der Daten zu falschen Schlussfolgerungen führen kann. Hier möchte ich nun eine Darstellungsvariante aufgreifen, mit der eine Vielzahl an Informationen darstellbar ist und dennoch ein gewisses Maß an Übersichtlichkeit gewahrt bleibt. RDI steht dabei für Rohdaten, deskriptive Statistik und Inferenz. Es werden also die einzelnen Datenpunkte dargestellt (im Beispiel: einzelne Punkte) sowie Elemente einer beschreibenden Statistik, wie der Mittelwert (im Beispiel: dickere horizontale Linie) oder der Median sowie die Verteilung der Daten (im Beispiel: Violinplot). Außerdem ist das sogenannte “95% High Density Interval” angegeben (im Beispiel: Box um den Mittelwert herum). Wir können uns also anhand der zugrunde liegenden Daten zu 95% sicher sein, dass der Mittelwert im angegeben Interval liegt. Für jedes einzelne Element lässt sich ein separater Transparenzwert angeben. Sind einem zum Beispiel die Einzelwerte in der Darstellung wichtiger, so reduziert man einfach die Transparenz der Punkte.
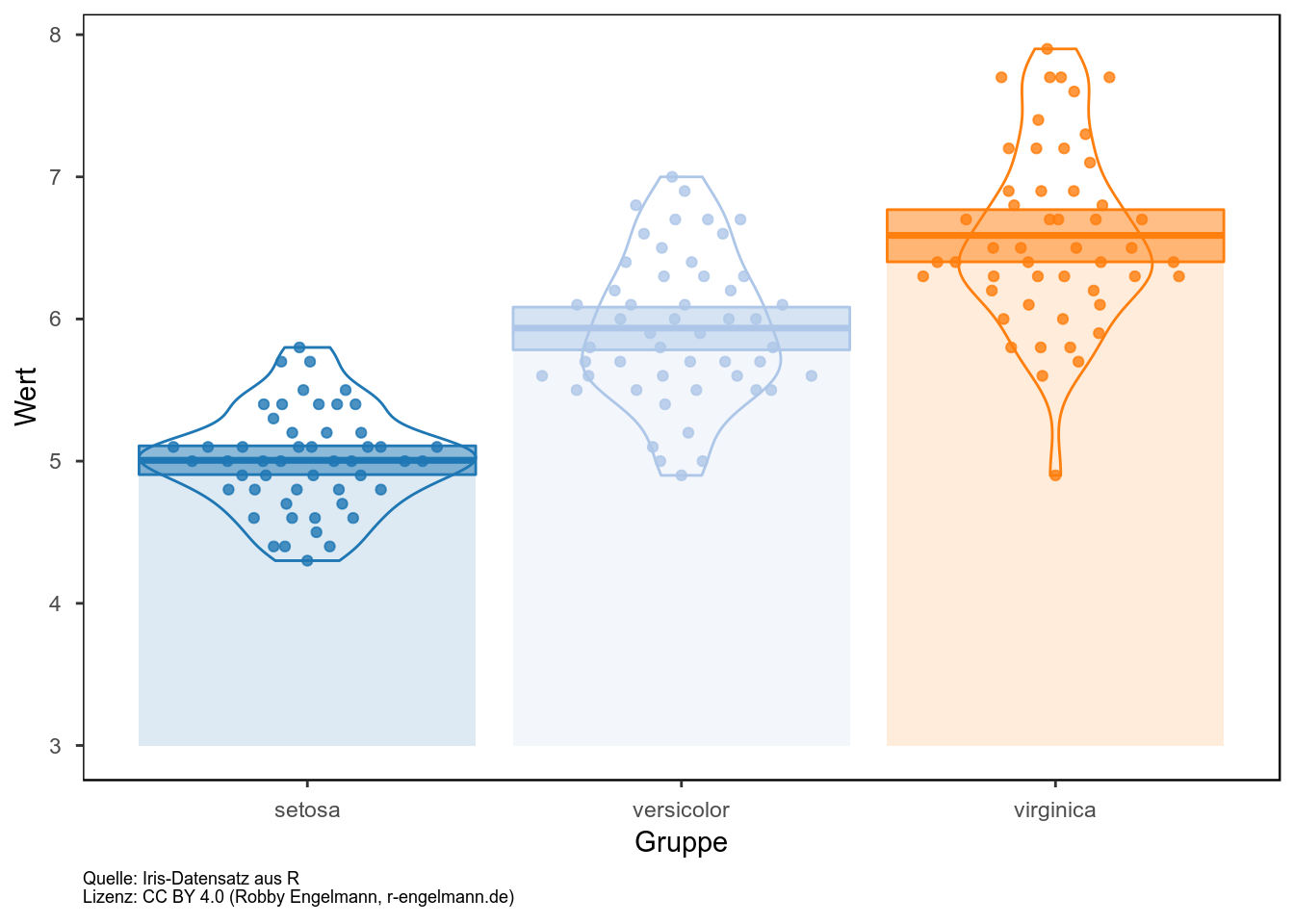
Horizontplot
Der Horizontplot eignet sich besonders zur vergleichenden Darstellung von Zeitverläufen. In seiner ursprünglichen Variante [http://lenkiefer.com/2017/04/23/horizon] wird dabei sowohl ein Werteanstieg als auch ein Werteabfall in den positiven Wertebereich projiziert und durch eine Farbkodierung zwischen Anstieg und Abfall unterschieden. Zusätzlich wird das Ausmaß der Veränderung über die Zeit in drei Bereiche aufgeteilt (geringe, mittlere und starke Veränderung). Alle Elemente werden dann in einen engen Bereich projiziert.
Ich möchte hier eine vereinfachte Form präsentieren, die meiner Meinung nach das Ziel des Horizontplots ebenfalls verwirklicht. Dabei wird die Größe des Anstiegs bzw. Abfalls einfach als Farbgradient kodiert. Als Beispiel habe ich die rollierenden 30-Tage Änderungen von einigen ETFs dargestellt.
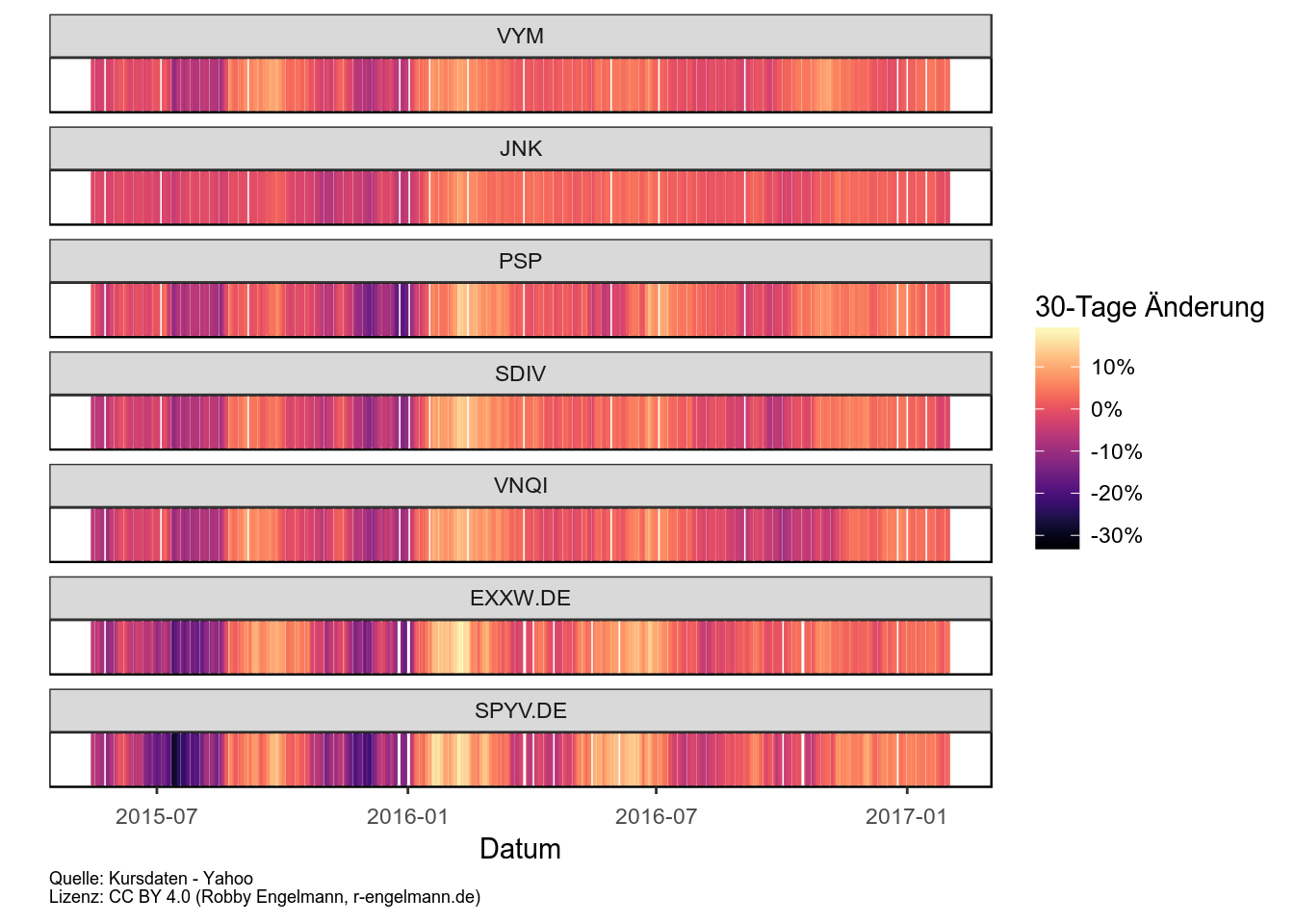
Referenzen
Datenquellen
Die hier verwendeten Kursdaten stammen von Yahoo Finance
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing.
R Foundation for Statistical Computing, Vienna, Austria. version 3.4.0 https://www.R-project.org/..
- Kate - Advanced Text Editor Version 17.04.1 (entwickelt von der KDE Community) http://kate-editor.org
- John K. Kruschke and Mike Meredith (2015). BEST: Bayesian Estimation
Supersedes the t-Test. R package version 0.4.0. https://CRAN.R-project.org/
package=BEST
- JAGS (Just Another Gibbs Sampler). It is a program for analysis of Bayesian
hierarchical models using Markov Chain Monte Carlo (MCMC) simulation. version
4.2.0 http://mcmc-jags.sourceforge.net/
- Hadley Wickham (2016). scales: Scale Functions for Visualization. R package
version 0.4.1. https://CRAN.R-project.org/package=scales
- Erik Clarke and Scott Sherrill-Mix (2016). ggbeeswarm: Categorical Scatter
(Violin Point) Plots. R package version 0.5.3. https://CRAN.R-project.org/
package=ggbeeswarm
- Hadley Wickham (2017). tidyverse: Easily Install and Load 'Tidyverse'
Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables
(Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for
'ggplot2'. R package version 3.4.0. https://CRAN.R-project.org/
package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version
0.17. https://CRAN.R-project.org/package=extrafont
- Simon Garnier (2016). viridis: Default Color Maps from 'matplotlib'. R
package version 0.4.0 https://CRAN.R-project.org/package=viridis
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff
Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic
Documents for R. R package version 1.4 https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
Kaufpreise von Wohnungen in Rostock
Datum: 04.05.2017
Kaufpreise Rostock
Im ersten Blogpost zu Rostocker Daten habe ich die aktuellen Mietpreisangebote dargestellt. Heute werde ich analog dazu die Kaufpreise anschauen. Auch dabei stammen die Daten von Immobilienscout24 und sind Bruttokaufpreise, also ohne Einberechnung von Kaufnebenkosten, wie Maklergebühren oder Grundbucheintragungen etc. Die Daten sind vom 8.4.2017 und schließen pro Ortsteil folgende Anzahl an Angeboten ein:
| Brinckmansdorf |
5 |
| Evershagen |
4 |
| Gehlsdorf |
7 |
| Hansaviertel |
17 |
| Hohe Düne |
5 |
| Kröpeliner-Tor-Vorstadt |
32 |
| Lichtenhagen |
9 |
| Lütten Klein |
27 |
| Reutershagen |
12 |
| Seebad Warnemünde |
23 |
| Stadtmitte |
14 |
| Südstadt |
3 |
| Toitenwinkel |
5 |
Die einzelnen Kaufangebote sind in der folgenden interaktiven Grafik dargestellt. Jeder Punkt ist ein Angebot. Wenn Sie mit dem Mauszeiger über die einzelnen Angebote fahren bekommen Sie Informationen über das jeweilige Angebot angezeigt. Für das teuerste Angebot in Warnemünde sehen Sie z.B., dass es sich um eine Penthousewohnung mit Ostseeblick handelt. Außerdem können Sie einzelne Bereiche der Abbildung markieren, um diese zu vergrößern. So sind z.B. die einzelnen Angebote für Lütten Klein kaum zu erkennen. Ziehen wir ein Kästchen herum, können wir uns nun die Daten für die einzelnen Angebote betrachten.
Kartendarstellung der Kaufpreise
Hier nun die Kartendarstellung der Bruttokaufpreise pro Quadratmeter. Dargestellt sind farbkodiert die medianen Bruttokaufpreise nach Stadtteil. Je dunkler die Farbe des Stadtteils desto höher der mediane Bruttokaufpreis. Für die grauen Gebiete sind keine oder zu wenige Daten für die Auswertung verfügbar gewesen.

Für die bessere Vergleichbarkeit mit anderen Darstellungen sind in der nächsten Abbildung die entsprechenden Durchschnittswerte dargestellt.

Vergleich mit den Mietpreisen und anderen Anlageklassen
Als letztes möchte ich mir noch zwei einfache Kennzahlen anschauen. Dies sind die Anzahl der Jahre bis man durch Vermietung den bezahlten Kaufpreis wieder rein hat. Dies spiegelt im Prinzip das Kurs-Gewinn-Verhältnis (KGV) von Aktienanlagen wider. Außerdem die Bruttorendite, die sich aus der durchschnittlichen Jahreskaltmiete durch den mittleren Kaufpreis pro Stadtviertel berechnet.
Für viele Stadtteile sind nur recht wenige Angebote vorhanden gewesen:
| Diedrichshagen |
2 |
1 |
3.30 |
30 |
| Dierkow-Neu |
86 |
1 |
5.56 |
18 |
| Evershagen |
101 |
4 |
5.49 |
18 |
| Gehlsdorf |
6 |
7 |
2.20 |
45 |
| Groß Klein |
111 |
1 |
6.07 |
16 |
| Hansaviertel |
26 |
17 |
2.88 |
35 |
| Kröpeliner Tor Vorstadt |
113 |
32 |
3.83 |
26 |
| Lichtenhagen |
87 |
9 |
3.29 |
30 |
| Lütten Klein |
77 |
27 |
4.93 |
20 |
| Reutershagen |
32 |
12 |
4.39 |
23 |
| Seebad Warnemünde |
23 |
23 |
1.96 |
51 |
| Stadtmitte |
114 |
14 |
3.08 |
33 |
| Südstadt |
16 |
3 |
5.81 |
17 |
| Toitenwinkel |
83 |
5 |
4.21 |
24 |
Daher habe ich diejenigen gefiltert, bei denen für die Berechnungen der mittleren Preise jeweils mindestens zehn Angebote verfügbar waren. Im folgenden Chart dargestellt sind die Kurs-Gewinn-Verhältnisse (KGV) dieser Stadtviertel aber auch die KGVs von verschiedenen anderen Anlageklassen. Für Geldanlagen kann man das KGV nutzen, um zu bewerten, ob ein Anlageprodukt fair, unter- oder auch überbewertet sein könnte. Das größte KGV zeigen bei unserer Analyse die Immobilien in Warnemünde. Dort müsste man im Schnitt 50 Jahre vermieten bis sich der Kaufpreis amortisiert hat. Und dabei ist die Berechnung noch sehr naiv, es werden weder Kaufnebenkosten noch Instandhaltungsmaßnahmen etc. eingerechnet.
Im Vergleich dazu hat der amerikanische Aktienmarkt (S&P 500), der momentan als eher teuer gilt, fast moderate Bewertungen. REITs (Real Estate Investment Trusts) dienen hier als Vergleich für die Anlageklasse Immobilien. REITs sind Aktiengesellschaften, die speziell im Immboliensektor investieren und fast die kompletten Gewinne wieder an die Anteilseigner ausschütten müssen. Ein globaler REIT ETF kommt auf ein KGV von 23 und liegt damit gleichauf mit Reutershagen. Mit im teuren Bereich liegen weiter die Stadtmitte und das Hansaviertel. Für die beiden Ortsteile kann man vermuten, dass die Mieten weniger stark angestiegen sind als die Kaufpreise. In der KTV scheint dies nicht der Fall zu sein, da die Bewertung durch das KGV geringer ausfällt.
Wenn man einen Immobilienkauf als Renditeobjekt anvisiert, kann man so durchaus Stadtviertel identifizieren, in denen es momentan im Durchschnitt eher zu teuer sein dürfte zu investieren. Allerdings kann dies niemand mit Sicherheit vorhersagen. Denn nicht nur die Mietrenditen muss man betrachten, sondern auch die Wertentwicklung der Immobilie. Die Preise könnten durchaus noch weiter steigen, aber genauso gut in wenigen Jahren zu fallen beginnen. Von stetig steigenden Preisen auszugehen, wie es viele zu tun scheinen, finde ich jedenfalls ziemlich naiv.

Referenzen
Datenquellen
- Die hier verwendeten Daten zu den Kauf- und Mietpreisangeboten stammen von Immobilienscout24 (Stand: 14.03.2017 für die Mietpreise und 08.04.2017 für die Kaufpreise).
- Das Kartenmaterial ist von Stamen Design, unter CC BY 3.0 lizensiert. Die Daten dort stammen von OpenStreetMap und sind unter ODbL lizensiert.
- Die Daten zu den Stadtteilgrenzen stammen von OpenData.HRO und unterliegen der CC0 1.0.
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.3.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 17.04.80 (entwickelt von der KDE Community) http://kate-editor.org
- David Robinson (2017). broom: Convert Statistical Analysis Objects into Tidy Data Frames. R package version 0.4.2. https://CRAN.R-project.org/package=broom
- Hadley Wickham (2016). rvest: Easily Harvest (Scrape) Web Pages. R package version 0.3.2. https://CRAN.R-project.org/package=rvest
- Hadley Wickham (2017). stringr: Simple, Consistent Wrappers for Common String Operations. R package version 1.2.0. https://CRAN.R-project.org/package=stringr
- Roger Bivand, Tim Keitt and Barry Rowlingson (2016). rgdal: Bindings for the Geospatial Data Abstraction Library. R package version 1.2-6. https://CRAN.R-project.org/package=rgdal
- Roger Bivand and Nicholas Lewin-Koh (2017). maptools: Tools for Reading and Handling Spatial Objects. R package version 0.9-2. https://CRAN.R-project.org/package=maptools
- D. Kahle and H. Wickham. ggmap: Spatial Visualization with ggplot2. The R Journal, 5(1), 144-161. URL http://journal.r-project.org/archive/2013-1/kahle-wickham.pdf
- Carson Sievert, Chris Parmer, Toby Hocking, Scott Chamberlain, Karthik Ram, Marianne Corvellec and Pedro Despouy (2016). plotly: Create Interactive Web Graphics via ‘plotly.js’. R package version 4.5.6. https://CRAN.R-project.org/package=plotly
- Erik Clarke and Scott Sherrill-Mix (2016). ggbeeswarm: Categorical Scatter (Violin Point) Plots. R package version 0.5.3. https://CRAN.R-project.org/package=ggbeeswarm
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- Simon Garnier (2016). viridis: Default Color Maps from ‘matplotlib’. R package version 0.4.0 https://CRAN.R-project.org/package=viridis
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.4 https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
Benchmarking und Risikokennzahlen
Datum: 12.04.2017
Zusammensetzung des Portfolios
Im ersten Blogpost zum Thema Finanzen haben wir uns Kurs- versus Performance-Charts der vorgestellten ETF’s angeschaut. Im zweiten Post kam die Analyse der Korrelationen hinzu. Hier wollen wir den einzelnen Positionen noch eine Gewichtung verleihen und das Portfolio als Ganzes betrachten.

Kennzahlen
Für die Berechnung der hier vorgestellten Portfoliokennzahlen wurde als Zeitraum die letzten drei Jahre zu Grunde gelegt. Alle hier vorgestellten Kennzahlen sind rückwärts gerichtet. Das heißt man berechnet sie aus den Preisen der Vergangenheit und man muss immer daran denken, dass dies keine Garantie für die Zukunft ist.
Alpha und Beta
Der Alpha-Wert eines Portfolios bezieht sich auf das Mehr an Rendite, die ein Portfolio im Vergleich zum Gesamtmarkt erwirtschaftet. Man hat z.B. zwei global anlegende Aktienportfolios. Eines erwirtschaftete 8% Rendite und das andere 5%. Als Vergleichswert könnte man hier den All-Country World Index (ACWI) heranziehen, der im selben Zeitraum vielleicht 6% Rendite ergab. So ist der Alpha-Wert des ersten Portfolios +2% und der des Zweiten -1%.
Der Beta-Wert beschreibt dagegen die Volatilität, also die Stärke der Preisschwankungen eines Portfolios verglichen mit dem Gesamtmarkt. Dabei entspricht ein Wert von 1 der Erwartung aus dem Gesamtmarkt. Ein Wert unter 1 bedeutet, dass das Portfolio weniger Preisschwankungen aufweist als der Gesamtmarkt (oder ein Vergleichsportfolio).
Während ein positives Alpha immer erstrebenswert ist, kann man das Beta nicht so einfach bewerten. Risiko-averse Investoren bevorzugen ein geringes Beta. Doch einige Investoren nehmen ein höheres Beta in Kauf, in der Hoffnung höhere Gewinne mitzunehmen oder besser in einen Markt einsteigen zu können.
Für die Berechnung der folgenden Alpha- und Beta-Werte diente der bereits oben erwähnte All-Country World Index (ACWI) als Vergleich.
Wie wir sehen, liegt der Alpha-Wert des untersuchten Portfolios im positiven Bereich, es erwirtschaftet also eine Mehrrendite verglichen mit dem ACWI und dass obwohl es nicht ausschließlich aus Aktien besteht, sondern auch einen Anteil von 23% an Anleihen und 11% an Rohstoffen enthält, für die eine geringere langfristige Rendite im Vergleich zu Aktien erwartet werden kann. Eine besonders große Out-Performance zeigt der IUS7.DE, ein Index auf in Dollar notierte Staatsanleihen der Entwicklungsländer.

Bei der Volatilität liegt unser Beispielportfolio deutlich unter 1. Dies bedeutet es weist eine geringere Volatilität im Vergleich zum ACWI auf.Auch hier fällt der IUS7.DE sehr positiv mit einer geringen Volatilität auf. Insgesamt kann man also sagen, dass unser Beispielportfolio eine Mehrrendite bei geringerer Schwankungsintensität erwirtschaftet verglichen mit dem ACWI.

Value-at-Risk
Der Value at Risk Wert bezieht sich auf die Verlustwahrscheinlichkeit. Für die hier durchgeführte Berechnung bedeutet der Wert folgendes: In fünf von 100 Monatsintervallen muss man mit dem jeweils angegebenen Verlust rechnen.
Unser Beispielportfolio liegt auch hier recht weit vorn, wenn wir es mit den jeweiligen Einzelpositionen des Portfolios vergleichen. Es folgt nur knapp nach den Anleihen-ETF’s (EUNW.DE, IUS7.DE und JNK), von denen man auch eine größere Preisstabilität erwarten würde. 
Maximaler Drawdown
Der maximale Drawdown bezeichnet den maximalen Verlust, den man mit dem jeweiligen Anlageprodukt im Untersuchungszeitraum erleiden musste. Auch hier liegt unser Beispielportfolio im oberen Bereich. 
Visualisierung der Returns
Nach den Kennzahlen für unser Portfolio, wollen wir uns nun anschauen, wie sich eine Anlage von 10.000€ in den letzten 10 Jahren hypothetisch entwickelt hätte. Dies betrachten wir im Vergleich zum Gesamtaktienmarkt (ACWI) und im Vergleich zu ETF’s, die spezielle Sektoren oder Regionen abbilden.
Gegen den globalen Aktienmarkt
Beim Vergleich mit dem ACWI fällt auf, dass unser Portfolio in der Phase der Finanzkrise von 2008 deutlich weniger Verluste erlitten hat als der globale Aktienmarkt. Dafür war der Preisanstieg zwischen den Jahren 2012 und 2015 weniger stark ausgefallen. Am Ende bleibt ein Plus von 1.130 €.

Gegen eine Auswahl an globalen Sektoren-ETF’s
Es folgt der Vergleich mit einer Auswahl an ETF’s, die global in definierte Sektoren anlegen.
Die folgenden ETF’s wurden für den Vergleich herangezogen:
| RXI |
zyklische Konsumgüter |
| KXI |
nicht-zyklische Konsumgüter |
| IXC |
Energie |
| IXG |
Finanzwesen |
| IXJ |
Gesundheit |
| EXI |
Industrie |
| MXI |
Materialien |
| IXN |
Technologie |
| JXI |
Versorger |
| IXP |
Telekommunikation |
| HAP |
Rohstoffunternehmen |
| RWO |
Immobilien |
Man sieht, dass die Finanzbranche in der Finanzkrise 2008 deutlich verloren hat und diesen Verlust auch bis heute nicht aufholen konnte. Die Energie-Branche verläuft lange Zeit recht parallel zu unserem Portfolio. Erst ab ca. 2015 zeigt sich ein Einbruch der Preise. Die Firmen aus dem Gesundheitssektor dagegen verteuerten sich ab 2014 deutlich stärker und liegen heute klar vor dem Portfolio. Auch die nicht-zyklischen Konsumgüter und die Technologie-Branche landen am Ende deutlich vor unserem Beispielportfolio.

Gegen eine Auswahl an Regionen
Folgende ETF’s für die jeweiligen Regionen wurden verwendet:
| EEM |
Emerging Markets |
| EWJ |
Japan |
| ILF |
Lateinamerika |
| GMF |
Asia-Pazifik |
| ADRU |
Europa |
| SPY |
US |
| FXI |
China |
| AFK |
Afrika |
Im Hinblick auf den Regionen-Vergleich liegt das Beispielportfolio mit Ausnahme USA und des Asia-Pazifik-Raum klar vorn.

Referenzen
Datenquellen
- Die Preisdaten der ETF’s stammen von Yahoo
- Die Dividendendaten der ETF’s stammen von Yahoo oder von den Webseiten der jeweiligen Emittenten
- Die Wechselkurse EUR/USD stammen von https://fred.stlouisfed.org/series/DEXUSEU
Werkzeuge
- Matt Dancho and Davis Vaughan (2017). tidyquant: Tidy Quantitative Financial Analysis. R package version 0.5.0. https://CRAN.R-project.org/package=tidyquant
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.3.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 17.03.80 (entwickelt von der KDE Community) http://kate-editor.org
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.3. https://CRAN.R-project.org/package=rmarkdown
Haftungsausschluss: Die hier dargestellten Finanzprodukte stellen keine Kaufempfehlung dar. Der Blog dient ausschließlich der Visualisierung von Daten und bietet keine Finanzberatung. Alle hier erwähnten Finanzprodukte sind nur ausgewählte Beispiele
↑ nach oben
Korrelation von Portfolio-Positionen
Datum: 07.04.2017
Warum wir wissen sollten, wie unsere Portfolio-Positionen korreliert sind
Korrelation im Allgemeinen beschreibt den Zusammenhang zweier Wertepaare. Zum Beispiel wird jemand, der größer ist, auch mehr wiegen. Größe und Gewicht von Personen sind also positiv miteinander korreliert. Wie stark dieser Zusammenhang ist, wird durch den sogenannten Korrelationskoeffizienten beschrieben. Ist dieser gleich 1, so gibt es einen perfekten positiven Zusammenhang (je größer, desto größer). Bei einem Korrelationskoeffizienten von 0 gibt es keinen Zusammenhang und ist er -1, so bedeutet dies einen perfekten negativen Zusammenhang (je größer, desto kleiner).
Bezogen auf die Bestandteile eines Portfolios von Vermögenswerten bedeutet ein Korrelationskoeffizient von 1, dass die Preise zweier Vermögenswerte über die Zeit vollkommen identisch verlaufen. Fällt der Preis eines Vermögenswertes um 50%, so gilt dies auch für den anderen Vermögenswert. Ein Korrelationskoeffizient von -1 würde bedeuten, dass der Preis des einen um 50% fällt, gleichzeitig der des anderen aber um 50% steigt.
Hat man ein Portfolio aus mehreren Vermögenswerten, so schwanken diese über die Zeit. Über einen langen Zeitraum erwirtschaftet jeder Vermögenswert eine gewisse durchschittliche Rendite pro Jahr. Doch diese durchschittliche Rendite kann nicht in jedem Jahr vereinnahmt werden. Es kann auch Jahre unter- bzw. überdurchschnittlicher Renditen geben. Ziel eines diversifizierten Portfolios ist es, diese Schwankungen möglichst gut auszugleichen, um das Verlustrisiko zu minimieren.
In diesem Blogeintrag stelle ich daher die Korrelationen der Bestandteile meines Beispiel-Portfolios aus dem letzten Blogeintrag dar.
Übersicht der Korrelation aller Portfolio-Positionen
Für die Berechnung der Korrelationskoeffizienten habe ich die Dividenden-adjustierten Preise, also die Gesamtperformance der ETF’s, genutzt. Aus diesen habe ich die monatlichen und wöchentlichen rollierenden Renditen berechnet und die Korrelationskoeffizienten über ein Fenster von 20 Handelstagen berechnet.
Monatliche rollierende Renditen
Für die Darstellung als Korrelationsmatrix habe ich aus den rollierenden Korrelationskoeffizienten der letzten zehn Jahre (bzw. seit Auflage der jeweiligen ETF’s) den Median gebildet und farbkodiert dargestellt:

Man kann auf der Diagonalen die Paarungen der jeweils gleichen Vermögenswerte erkennen. Erwartungsgemäß zeigen diese eine vollständige positive Korrelation. Gold (GLD) und Silber (DBS) sind am geringsten mit den anderen ETF’s korreliert, aber stark miteinander. Auch das entspricht der Erwartung. Außerdem fällt der IUS7.DE auf, denn auch er zeigt eine eher geringe Korrelation mit vielen der anderen ETF’s.
In der Matrix kann man sich insgesamt eine gute Übersicht darüber verschaffen, welche Vermögenswerte einen Beitrag zur Diversifikation des Portfolios leisten und welche eher nicht. Dabei kann man noch den betrachteten Zeitraum anpassen, z.B. auf das letzte Jahr begrenzen, wenn man nur die aktuellen Werte mit einbeziehen möchte.
Wöchentliche rollierende Renditen
Hier die entsprechende Abbildung für die wöchentlichen rollierenden Renditen:

Diese unterscheiden sich ein wenig, geben aber insgesamt das Bild der monatlichen Renditen wider.
Zeitlicher Verlauf
Da sich die Korrelationen der Vermögenswerte dynamisch über die Zeit verändern können, sollte man sich nicht nur einen statischen Wert, sondern auch die Veränderung über die Zeit anschauen.
Monatliche rollierende Renditen
Dies machen wir im Folgenden am Beispiel einiger ausgewählter Portfolio-Positionen für die monatlichen rollierenden Renditen:

Hier kann man sehen, dass analog zur einfachen Korrelationsmatrix auf der Diagonalen (Vergleich der gleichen Vermögenswerte) erwartungsgemäß eine vollkommene Korrelation im Form einer horizontalen Geraden bei 1 vorliegt. Schauen wir uns den zeitlichen Verlauf für Gold (GLD) an, so sehen wir z.B. eine Abschwächung des Zusammenhangs mit dem EL4X.DE seit ca. 2015 bis 2016, wobei seit einiger Zeit wieder ein Anstieg zu sehen ist.
Mittels zeitlichen Verlauf kann man sich also ein Bild darüber machen, ob ein Vermögenswert im Portfolio in den vergangenen Jahren besser oder schlechter zur Diversifikation beiträgt. Oder aber auch wie sich der Beitrag zur Diversifikation unter bestimmten Marktbedingungen ändern kann.
Wöchentliche rollierende Renditen
Der Vollständigkeit halber hier noch die entsprechende Abbildung für die wöchentlichen Renditen:

Referenzen
Datenquellen
- Die Preisdaten der ETF’s stammen von Yahoo
- Die Dividendendaten der ETF’s stammen von Yahoo oder von den Webseiten der jeweiligen Emittenten
- Die Wechselkurse EUR/USD stammen von https://fred.stlouisfed.org/series/DEXUSEU
Werkzeuge
- Matt Dancho and Davis Vaughan (2017). tidyquant: Tidy Quantitative Financial Analysis. R package version 0.4.0. https://CRAN.R-project.org/package=tidyquant
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.3.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 16.12.2 (entwickelt von der KDE Community) http://kate-editor.org
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.3. https://CRAN.R-project.org/package=rmarkdown
Haftungsausschluss: Die hier dargestellten Finanzprodukte stellen keine Kaufempfehlung dar. Der Blog dient ausschließlich der Visualisierung von Daten und bietet keine Finanzberatung. Alle hier erwähnten Finanzprodukte sind nur ausgewählte Beispiele
↑ nach oben
Preisverlauf und Charts von Portfolio-Positionen
Datum: 02.04.2017
Zusammensetzung des Portfolios
Das Portfolio, das ich hier in diesem Blog darstellen werde, basiert auf ETFs und bildet festgelegte Regionen und Sektoren ab. Es ist darauf ausgerichtet eine möglichst hohe Ausschüttungsrendite zu erwirtschaften. Das Portfolio besteht aus folgenden Finanzprodukten:
| GLD |
Gold |
| DBS |
Silver |
| ISPA.DE |
iShares STOXX Global Select Dividend 100 |
| SDIV |
Global X SuperDividend ETF |
| EL4X.DE |
ETFlab DAXplus® Maximum Dividend |
| VYM |
Vanguard High Dividend Yield ETF |
| EXSH.DE |
iShares STOXX Europe Select Dividend 30 (DE) |
| EUNW.DE |
iShares Markit IBoxx Euro High Yield |
| IUS7.DE |
iShares JPMorgan $ Emerging Markets Bonds |
| JNK |
SPDR Barclays High Yield Bond ETF |
| VNQI |
Vanguard Global ex US Real Estate ETF |
| SRET |
Global X SuperDividend REIT ETF |
| EXXW.DE |
iShares DJ Asia Pacific Select Dividend 30 |
| SPYV.DE |
SPDR S&P Emerging Markets Dividend ETF |
| PSP |
PowerShares Global Listed Private Equity Portfolio |
Prozentuales Wachstum mit und ohne Ausschüttungen (Kurs- versus Performanceindices)
Daten direkt von Yahoo
Als erstes möchte ich von den Anlageprodukten die Preis- und Performance-Charts über einen längeren Zeitraum darstellen. Hier nutze ich über das Zusatzpaket tidyquant die Preisdaten von Yahoo Finanzen. Die Preise sind die jeweiligen Schlusskurse der Finanzanlagen, d.h. die reinen Kursdaten ohne Einberechnung der Ausschüttungen der ETF’s. Für den Performance-Chart, bei dem die Ausschüttungen mit eingerechnet sind, nutze ich zunächst die Dividenden-adjustierten Preise von Yahoo:

Beim Betrachten der Grafik fällt Kennern dieser Finanzprodukte schnell auf, dass die Performance-Charts z.T. nicht korrekt sein können. Für DBS und GLD entspricht der Preis-Chart dem Performance-Chart, was korrekt ist, da Gold und Silber natürlich keine Dividenden auszahlen. Für IUS7.DE und SPYV.DE sind beide Charts jedoch auch identisch und für EXXW.DE, EL4X.DE und EXSH.DE divergieren die beiden Charts erst recht spät. Da alle diese ETFs ausschüttend sind, erwartet man hier einen deutlichen Unterschied zwischen Preis und Performance-Chart. Wo liegt hier das Problem?
Einberechnung der korrekten Dividendendaten in die Performanceindices
Bei genauer Betrachtung der Dividenden-Daten von Yahoo fällt schnell auf, dass die Dividendenhistorie bei den ETF’s mit der Endung .DE, also den in Deutschland aufgelegten ETF’s, entweder komplett fehlt oder fehlerhaft ist. Daher musste ich für diese ETF’s die Dividenden manuell nachtragen und die Dividenden-adjustierten Preise für den Performance-Chart selbst berechnen. Dazu habe ich die Formel aus einem Blogeintrag des Trading Journals genutzt.
Hier nun die korrekte Grafik:

Andere Charttypen
Neben dem einfachen Linien-Chart gibt es noch zwei weitere Darstellungsvarianten der Preise, den Bar-Chart und den Candlestick-Chart. Beide Charts zeigen nicht nur den Schlusskurs, sondern geben auch den Startkurs sowie Höchst- und Tiefstpreise an.
Bar-Chart
Beim Bar-Chart oder OHLC-Chart zeigt das obere Ende der vertikalen Linie den Höchst- und das untere Ende den Tiefstkurs eines Zeitraumes an. Die beiden horizontalen Skalenstriche zeigen den Start- bzw. Schlusskurs an.
Im folgenden Beispiel ist der tägliche Kursverlauf des Vanguard High Dividend Yield ETF (VYM) der letzten 12 Wochen gezeigt:

Candlestick-Chart
Der Candlestick-Chart ist sehr ähnlich: die Boxen geben Start und Schlusskurse an, die Linien Höchst- und Tiefstkurse. Wie beim Bar-Chart ist grün gleich ein positiver und rot ein negativer Tagesverlauf.

Indikatorlinien
Gleitender Durchschnitt
Für die Einordnung der aktuellen Preise im zeitlichen Verlauf kann man bestimmte Durchschnittswerte nutzen, wie hier am Beispiel der einfachen gleitenden Durchschnitte gezeigt. Diese und die folgenden Bollinger Bänder werden in der Charttechnik verwendet, um zukünftige Kursverläufe abzuleiten. Hier auf diesem Blog konzentriere ich mich als langfristig orientierter Investor eher auf Elemente zur Analyse von Portfolios. Nichtsdestotrotz hier die gleitenden Durchschnitte:

Bollinger Bänder
Auch die Bollinger Bänder, hier der einfache gleitende Durchschnitt als mittlere Linie und die zweifachen Standardabweichung nach oben und unten dargestellt, werden hauptsächlich für die Charttechnik genutzt und hier nicht näher betrachtet.

Referenzen
Datenquellen
- Die Preisdaten der ETF’s stammen von Yahoo
- Die Dividendendaten der ETF’s stammen von Yahoo oder von den Webseiten der jeweiligen Emittenten
- Die Wechselkurse EUR/USD stammen von https://fred.stlouisfed.org/series/DEXUSEU
Werkzeuge
- Matt Dancho and Davis Vaughan (2017). tidyquant: Tidy Quantitative Financial Analysis. R package version 0.4.0. https://CRAN.R-project.org/package=tidyquant
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.3.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 16.12.2 (entwickelt von der KDE Community) http://kate-editor.org
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.3. https://CRAN.R-project.org/package=rmarkdown
Haftungsausschluss: Die hier dargestellten Finanzprodukte stellen keine Kaufempfehlung dar. Der Blog dient ausschließlich der Visualisierung von Daten und bietet keine Finanzberatung. Alle hier erwähnten Finanzprodukte sind nur ausgewählte Beispiele.
↑ nach oben
Kartendaten
Datum: 28.03.2017
Einleitung
Daten mit Bezug zu geografischen Gegebenheiten lassen sich natürlich auch mit den bereits vorgestellten Darstellungen von Gruppendaten visualisieren, da jeder Ortsteil natürlich auch eine Gruppe darstellt. Einprägsamer kann man ortsgebunde Daten oft mit Hilfe von Karten darstellen. Dies soll in diesem Blogeintrag anhand von Mietpreisdaten gezeigt werden.
Mietpreise in Rostock
Zunächst habe ich nach frei verfügbaren Mietpreisdaten gesucht, bin allerdings für Rostock leider nicht fündig geworden. Daher habe ich mich dazu entschlossen, die aktuellen und archivierten Angebotsdaten aus den Immobilienscout24 Suchergebnissen für Rostock zu verwenden. Die im Folgenden dargestellten Daten spiegeln also nicht die Bestandsmieten sondern die Angebotsmieten (Stand: 14.03.2017) wider.
Außerdem habe ich mich für die Berechnung der Durchschnittswerte pro Stadtviertel auf jene Viertel beschränkt, zu denen ich mindestens zehn Datenpunkte erhalten konnte. Stehen nur wenige Daten für ein Stadtviertel zur Verfügung, so sind die Durchschnittswerte nicht notwendigerweise repräsentativ. Folgende Anzahl an Angeboten nach Ortsteilen flossen in die Auswertung ein:
| Dierkow-Neu |
86 |
| Evershagen |
101 |
| Groß Klein |
111 |
| Hansaviertel |
26 |
| Kröpeliner-Tor-Vorstadt |
113 |
| Krummendorf |
11 |
| Lichtenhagen |
87 |
| Lütten Klein |
77 |
| Reutershagen |
32 |
| Schmarl |
66 |
| Seebad Warnemünde |
23 |
| Stadtmitte |
114 |
| Südstadt |
16 |
| Toitenwinkel |
83 |
In der ersten Darstellung habe ich mich für den Violinplot entschieden. Wie im Beitrag zur Visualisierung von Gruppendaten beschrieben, kann man in dieser Darstellung die Datenverteilung gut beurteilen. Die grauen Punkte geben jeweils den Median an.
Anhand der Verteilung der Angebotskaltmietpreise kann man grob zwei Gruppen von Stadtvierteln ausmachen. Einmal Viertel, wie Schmarl oder Lütten Klein, bei denen sich die Preise in einem engen Bereich um den Median herum bewegen. Daneben Viertel, wie Stadtmitte oder Kröpeliner Tor Vorstadt, die im Median teuerer sind aber auch eine sehr viel breitere Verteilung der Preise zeigen. Bei der KTV geht der Preisbereich für die Kaltmiete pro qm von 6€ bis fast 30€.

Für die Darstellung von ortsbezogenen Daten, wie hier die aktuellen Angebotskaltmieten der Hansestadt Rostock, bietet es sich an, Kartenmaterial zu verwenden. Diese Form der Präsentation der Daten ist besonders für ortskundige Betrachter anschaulicher. Einige Beispiele folgen nun.
Das Kartenmaterial
Zur Präsentation der Daten in Form von geografischen Karten benötigt man natürlich zunächst das entsprechende Kartenmaterial. Hier wurde auf Karten von maps.stamen.com zurückgegriffen, die letztlich auf dem Kartenmaterial von OpenStreetMaps beruhen. Zusätzlich möchte ich die Ortsteile von Rostock darstellen. Dafür gibt es sogenannte “shape-files”, in denen die Ortsteilgrenzen beschrieben sind.
Hier zunächst die Basiskarte von Rostock:

Und dazu die Ortsteile:

Sowie hier beides in Kombination:

Übersicht der Angebotsmietpreise
Hier nun die Kartendarstellung der Angebotsmietpreise. Die medianen Angebotsmietpreise nach Stadteil sind dabei farbkodiert. Je dunkler die Farbe des Stadtteils desto höher die mediane Kaltmiete pro qm. Für die grauen Gebiete sind entweder keine Daten oder weniger als zehn Angebote für die Auswertung verfügbar gewesen.

Zur besseren Vergleichbarkeit mit anderen Darstellungen der Mietpreise sind in der nächsten Abbildung die entsprechenden Durchschnittswerte dargestellt. Denn meist findet man eher Durchschnittswerte als Mediane.

Die Suchergebnisse bei Immobilienscout24 schließen auch Adressangaben mit ein, was es ermöglicht auch jedes Angebot separat darzustellen. In dieser Karte entspricht jeder Punkt einem Angebot, wobei auch hier die Farbe der Punkte den jeweiligen Preis für die Kaltmiete pro qm anzeigt.

Angebotsmietpreise im Stadtkern
Zuletzt zoomen wir in die Karte etwas hinein und betrachten lediglich den Stadtkern.


Interessant wäre jetzt noch zu sehen, wie sich die Mietpreise z.B. in den letzten drei Jahren entwickelt haben. Dazu kenne ich bisher noch keine Datenquelle, die es mir erlaubt dies zu veranschaulichen. Wenn Sie eine kennen, kontaktieren Sie mich doch einfach und ich werde die Daten hier in diesem Blog darstellen. Alternativ gedenke ich, in sechs bis zwölf Monaten mir die dann aktuellen Preise anzuschauen. Vielleicht ist eine Entwicklung ablesbar.
Fazit
Kartendarstellungen bieten besonders für Ortskundige einen anschaulicheren Zugang zu Daten. Allerdings geht bei der hier gewählten Visualisierung die Verteilung der jeweiligen Preise verloren. Doch auch dies wäre möglich in einer Karte zu zeigen. Wir merken uns also: die Zielgruppe definiert die Art und Weise der Darstellungsform.
Referenzen
Datenquellen
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.3.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 16.12.2 (entwickelt von der KDE Community) http://kate-editor.org
- David Robinson (2017). broom: Convert Statistical Analysis Objects into Tidy Data Frames. R package version 0.4.2. https://CRAN.R-project.org/package=broom
- Hadley Wickham (2016). rvest: Easily Harvest (Scrape) Web Pages. R package version 0.3.2. https://CRAN.R-project.org/package=rvest
- Roger Bivand, Tim Keitt and Barry Rowlingson (2016). rgdal: Bindings for the Geospatial Data Abstraction Library. R package version 1.2-5. https://CRAN.R-project.org/package=rgdal
- Roger Bivand and Nicholas Lewin-Koh (2017). maptools: Tools for Reading and Handling Spatial Objects. R package version 0.9-1. https://CRAN.R-project.org/package=maptools
- D. Kahle and H. Wickham. ggmap: Spatial Visualization with ggplot2. The R Journal, 5(1), 144-161. URL http://journal.r-project.org/archive/2013-1/kahle-wickham.pdf
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont
- Simon Garnier (2016). viridis: Default Color Maps from ‘matplotlib’. R package version 0.3.4. https://CRAN.R-project.org/package=viridis
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.3. https://CRAN.R-project.org/package=rmarkdown
↑ nach oben
Visualisierung von Daten unterschiedlicher Gruppen
Datum: 19.03.2017
In diesem Abschnitt möchte ich zeigen, wie man Daten verschiedener Gruppen visualisieren kann. In vielen Publikationen ist die am häufigsten verwendete Darstellung ein Balkendiagramm. Die Höhe der Balken gibt dabei den Mittelwert der Gruppe an und die Klammern nach oben und unten geben die Streuung um den Mittelwert an. Als statistische Maße werden dafür zumeist die Standardabweichung oder der Standardfehler benutzt. Nun ein Beispiel:
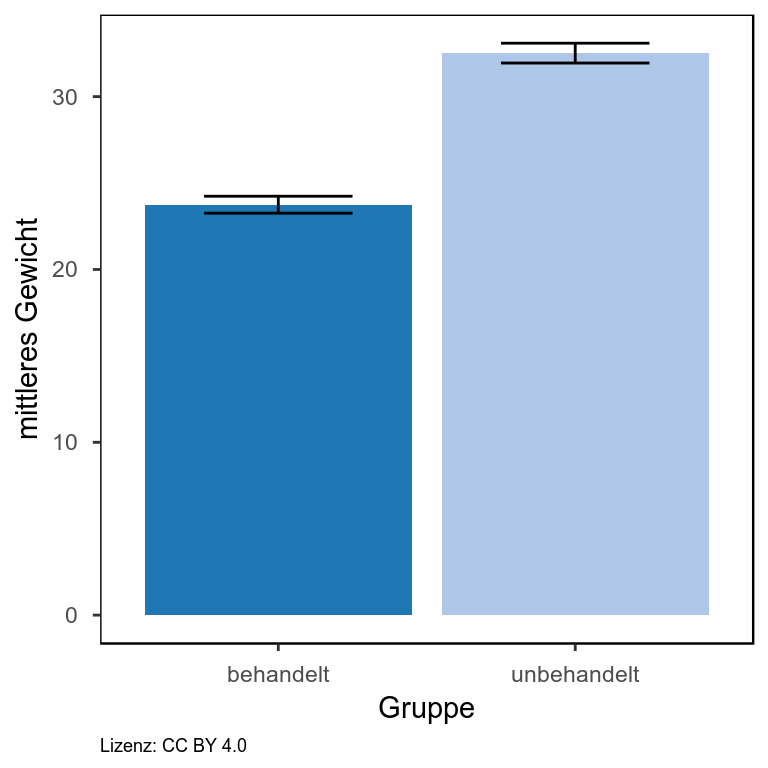 Gezeigt ist hier das Gewicht von zwei Gruppen von Tieren, Behandelte und unbehandelte Tiere. Wie man erkennen kann, wiegen die behandelten Tiere im Schnitt weniger als die Unbehandelten. Als Streuungsmaß ist hier der Standardfehler angegeben. Da dieser zwischen beiden Gruppen nicht überlappt, kann man davon ausgehen, dass der Unterschied im Gewicht beider Gruppen auch signifikant ist. Um dies zu belegen, würde man allerdings noch einen statistischen Test durchführen.
Gezeigt ist hier das Gewicht von zwei Gruppen von Tieren, Behandelte und unbehandelte Tiere. Wie man erkennen kann, wiegen die behandelten Tiere im Schnitt weniger als die Unbehandelten. Als Streuungsmaß ist hier der Standardfehler angegeben. Da dieser zwischen beiden Gruppen nicht überlappt, kann man davon ausgehen, dass der Unterschied im Gewicht beider Gruppen auch signifikant ist. Um dies zu belegen, würde man allerdings noch einen statistischen Test durchführen.
Wenn man sich an dem Grundsatz orientiert, das Verhältnis von Tinte zu Information zu optimieren, dann hält sich die Darstellung von Punkten und Streuung schon besser daran, wie man hier sehen kann:
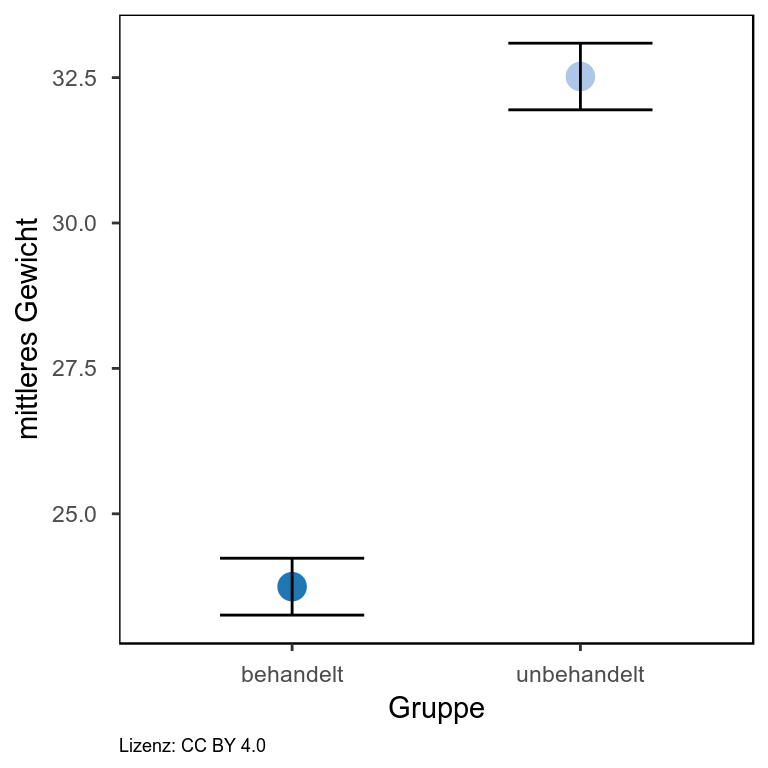 In diesem Punktediagramm sind die gleichen Werte wie im Balkendiagramm dargestellt, die Grafik wirkt jedoch aufgelockerter.
In diesem Punktediagramm sind die gleichen Werte wie im Balkendiagramm dargestellt, die Grafik wirkt jedoch aufgelockerter.
Soweit so gut. Aber was kann man nun alles in diesen beiden Grafik nicht ablesen? Wir können nicht erkennen, wieviele Tiere in jeder Gruppen untersucht worden. Wir können nichts über die Verteilung der Einzelwerte aussagen. Ist es hier überhaupt gerechtfertigt den Mittelwert zu verwenden, liegt also eine Normalverteilung der Daten vor. Und gibt es einzelne Ausreißer?
Um diese Fragen beantworten zu können gibt es an dieser Stelle eine Vielzahl von Darstellungsmöglichkeiten, die mehr Informationen bieten. Nehmen wir zunächt einmal einen Boxplot. Anhand des Boxplots kann man die Verteilung der Daten etwas besser abschätzen:
 Gezeigt ist hier der Median der Daten als horizontale Linie in der Box. Der Median gibt die Mitte der Daten wieder, d.h. die Hälfte der Werte ist größer als der Median und die andere Hälfte kleiner.
Gezeigt ist hier der Median der Daten als horizontale Linie in der Box. Der Median gibt die Mitte der Daten wieder, d.h. die Hälfte der Werte ist größer als der Median und die andere Hälfte kleiner.
Hier ein kurzes Beispiel: Hat man die drei Werte 1, 5 und 30, so ist der Mittelwert (1+5+30)/3 gleich 12, der Median ist der mittlere Wert, also in unserem Beispiel die 5. Daran sieht man, dass sich beide Werte stark unterscheiden. Hat man wenige sehr große Werte, so ziehen diese den Mittelwert mit nach oben, obwohl die Mehrheit der Werte eher im unteren Bereich ist. Der Median ist dafür weniger anfällig.
Aber zurück zum Boxplot. Dargestellt sind neben dem Median noch die Boxen an sich. Diese enthalten 75% der Daten und die Linien nach oben und unten von der Box ausgehend decken einen noch breiteren Bereich der Daten ab, welchen genau ist nicht eindeutig festgelegt und ist wählbar. Anhand des Boxplot, kann man die Verteilung der Werte also besser ablesen.
Eine weitere Variante ist der Violinplot, mit dem man die Datenverteilung noch genauer visualisieren kann:
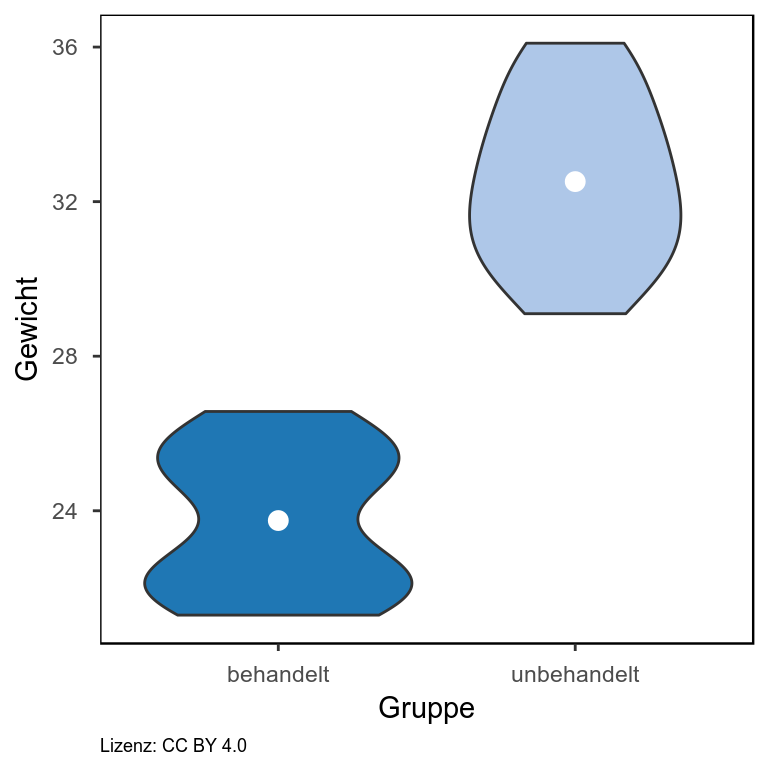 Man kann in diesem Violinplot erkennen, dass das Gewicht der unbehandelten Tiere ziemlich uniform um den Mittelwert (weißer Punkt) verteilt ist. Bei den behandelten Tiere sieht man zwei Bäuche in der Verteilung, d.h. es gibt eine Häufung von Daten einmal im oberen und einmal im unteren Wertebereich.
Man kann in diesem Violinplot erkennen, dass das Gewicht der unbehandelten Tiere ziemlich uniform um den Mittelwert (weißer Punkt) verteilt ist. Bei den behandelten Tiere sieht man zwei Bäuche in der Verteilung, d.h. es gibt eine Häufung von Daten einmal im oberen und einmal im unteren Wertebereich.
Nun schauen wir uns aber endlich an, wo jeder einzelne Datenpunkt genau liegt und wie viele Datenpunkte in jeder Gruppe zu vorhanden sind:
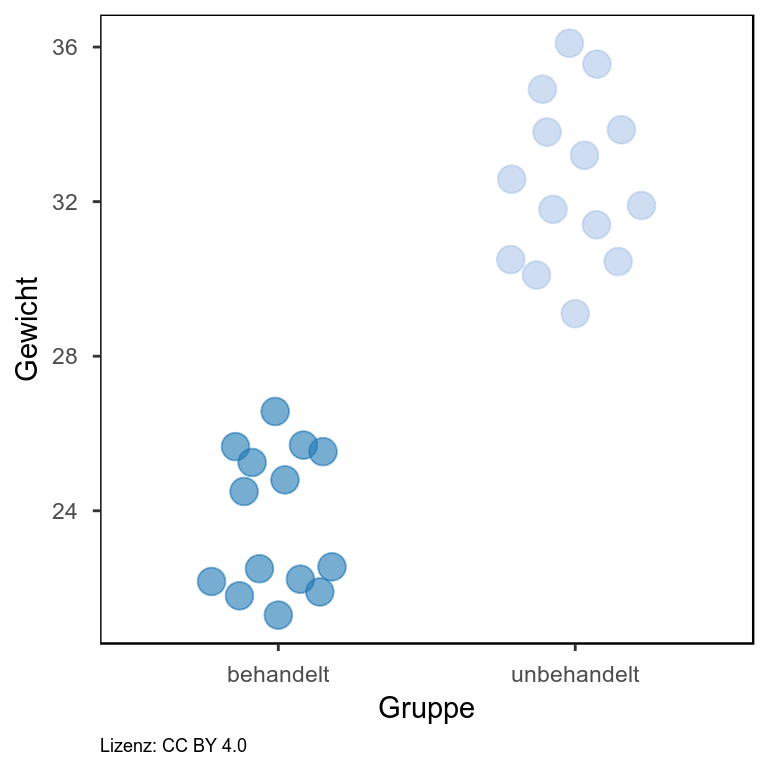 Dies ist gleichzeitig die Darstellung mit dem größten Informationsgehalt. Allerdings kann man sich vorstellen, dass die Darstellung der einzelnen Datenpunkte schnell sehr unübersichtlich wird, wenn über 30-50 Punkte in jeder Gruppe darzustellen sind.
Dies ist gleichzeitig die Darstellung mit dem größten Informationsgehalt. Allerdings kann man sich vorstellen, dass die Darstellung der einzelnen Datenpunkte schnell sehr unübersichtlich wird, wenn über 30-50 Punkte in jeder Gruppe darzustellen sind.
Alles in allem ist die Verwendung von Balkendiagrammen zwar gängige Praxis in vielen biomedizinischen Veröffentlichungen, doch es gibt (A) Alternativen, um die gleiche Information klarer darzustellen und (B) viele weitere Varianten der Darstellung, die mehr Informationen für den Leser bieten.
Auch hier ist man nicht am Ende der Darstellungsvarianten angekommen, denn man kann auch verschiedene Darstellungen miteinander kombinieren, z.B. den Boxplot und die Einzelwerte:
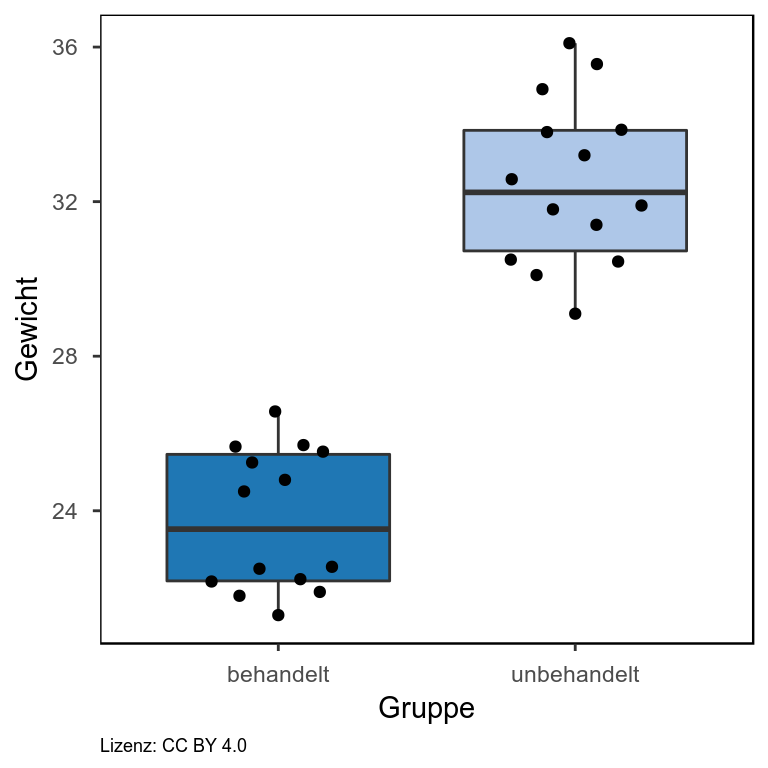
Man kann natürlich auch noch weitere Parameter in diese Darstellung einbinden:
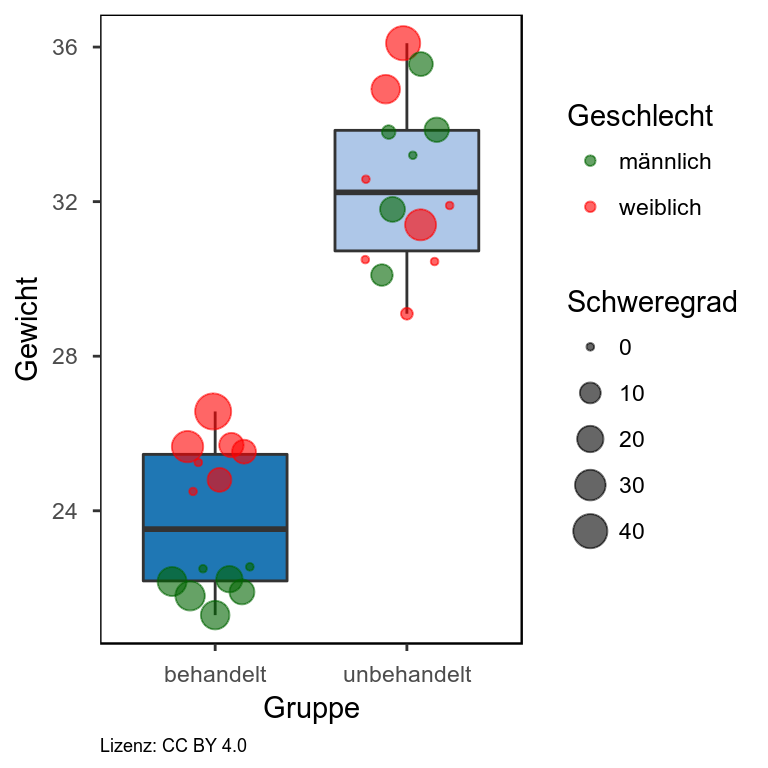 An diesem Beispiel sieht man, dass der Schweregrad sich kaum zwischen behandelt und unbehandelten Tieren unterscheidet. Auch wenn man sich nur die Behandelten betrachtet erklärt der Schweregrad nicht die beiden Gewichtsgruppen, wohl aber das Geschlecht. Zur Absicherung dieser Aussagen würde man natürlich die passenden statistischen Tests durchführen. Das soll aber hier nicht Thema sein.
An diesem Beispiel sieht man, dass der Schweregrad sich kaum zwischen behandelt und unbehandelten Tieren unterscheidet. Auch wenn man sich nur die Behandelten betrachtet erklärt der Schweregrad nicht die beiden Gewichtsgruppen, wohl aber das Geschlecht. Zur Absicherung dieser Aussagen würde man natürlich die passenden statistischen Tests durchführen. Das soll aber hier nicht Thema sein.
Referenzen
Datenquellen
Die hier verwendeten Daten habe ich selbst zusammengestellt, um die unterschiedlichen dargestellten Aspekte zu demonstrieren.
Genutzte Werkzeuge
- R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. version 3.3.3 https://www.R-project.org/.
- Kate - Advanced Text Editor Version 16.12.2 (entwickelt von der KDE Community) http://kate-editor.org.
- Hadley Wickham (2017). tidyverse: Easily Install and Load ‘Tidyverse’ Packages. R package version 1.1.1. https://CRAN.R-project.org/package=tidyverse.
- Hadley Wickham (2017). forcats: Tools for Working with Categorical Variables (Factors). R package version 0.2.0. https://CRAN.R-project.org/package=forcats.
- Jeffrey B. Arnold (2017). ggthemes: Extra Themes, Scales and Geoms for ‘ggplot2’. R package version 3.4.0. https://CRAN.R-project.org/package=ggthemes.
- Erik Clarke and Scott Sherrill-Mix (2016). ggbeeswarm: Categorical Scatter (Violin Point) Plots. R package version 0.5.3. https://CRAN.R-project.org/package=ggbeeswarm.
- Winston Chang, (2014). extrafont: Tools for using fonts. R package version 0.17. https://CRAN.R-project.org/package=extrafont.
- Simon Garnier (2016). viridis: Default Color Maps from ‘matplotlib’. R package version 0.3.4. https://CRAN.R-project.org/package=viridis.
- JJ Allaire, Joe Cheng, Yihui Xie, Jonathan McPherson, Winston Chang, Jeff Allen, Hadley Wickham, Aron Atkins and Rob Hyndman (2016). rmarkdown: Dynamic Documents for R. R package version 1.3. https://CRAN.R-project.org/package=rmarkdown.
↑ nach oben
Die Website geht an den Start
Datum: 19.03.2017
Nach einigen Monaten Vorbereitungszeit und Arbeit an der Seite sind wir nun soweit damit zufrieden, dass die Basiselemente stehen und wir die Seite für Sie online stellen möchten.
Auf R-Engelmann.de möchte ich kontinuierlich Möglichkeiten zur Datenvisualisierung und -analyse demonstrieren. In der heutigen Welt sind enorme Mengen an Daten frei verfügbar. Die Herausforderung ist diese Daten soweit zugänglich zu machen, dass man auch tatsächlich Informationen daraus ableiten kann.
Als Hilfsmittel werde ich ausschließlich Open-Source Werkzeuge nutzen und alle "Werke" unter einer Creative-Commons Lizenz stellen, sodass eine weitere Verwendung möglich sein wird. In den ersten Blogeinträgen plane ich anhand von einfachen Beispieldaten eine allgemeine Auswahl der Visualisierungsmöglichkeiten zu demonstrieren. Danach möchte ich etwas in die Tiefe gehen und mir regelmäßig aus bestimmten Bereichen spezielle Datensätze herauspicken, um eigene oder auch Ihre Fragestellungen zu beantworten. Diese Bereiche möchte ich dabei bearbeiten:
- Biomedizin
- Sozioökonomie
- Finanzportfolios
- ...
Wenn Sie als Leser selbst eine Fragestellung beziehungsweise einen Datensatz haben, können Sie mir gern eine Nachricht schreiben und ich versuche das entsprechend umzusetzen und in einem Blogbeitrag zu veröffentlichen.
Einige Funktionen sind bisher noch nicht implementiert und werden noch folgen:
- Kommentarfunktion
- Zweisprachigkeit (englisch und deutsch)
Ich selbst möchte die Zeit hier nutzen, um Visualisierungen und Analysen umzusetzen und daraus zu lernen. Mein Ziel ist es nach einiger Zeit bis zu interaktiven Webgrafiken und -anwendungen vorzudringen.
Was soll diese Seite nicht sein?
- Einführung in Statistik
- Tutorials für die verwendeten Werkzeuge
↑ nach oben



























 Gezeigt ist hier das Gewicht von zwei Gruppen von Tieren, Behandelte und unbehandelte Tiere. Wie man erkennen kann, wiegen die behandelten Tiere im Schnitt weniger als die Unbehandelten. Als Streuungsmaß ist hier der Standardfehler angegeben. Da dieser zwischen beiden Gruppen nicht überlappt, kann man davon ausgehen, dass der Unterschied im Gewicht beider Gruppen auch signifikant ist. Um dies zu belegen, würde man allerdings noch einen statistischen Test durchführen.
Gezeigt ist hier das Gewicht von zwei Gruppen von Tieren, Behandelte und unbehandelte Tiere. Wie man erkennen kann, wiegen die behandelten Tiere im Schnitt weniger als die Unbehandelten. Als Streuungsmaß ist hier der Standardfehler angegeben. Da dieser zwischen beiden Gruppen nicht überlappt, kann man davon ausgehen, dass der Unterschied im Gewicht beider Gruppen auch signifikant ist. Um dies zu belegen, würde man allerdings noch einen statistischen Test durchführen. In diesem Punktediagramm sind die gleichen Werte wie im Balkendiagramm dargestellt, die Grafik wirkt jedoch aufgelockerter.
In diesem Punktediagramm sind die gleichen Werte wie im Balkendiagramm dargestellt, die Grafik wirkt jedoch aufgelockerter. Gezeigt ist hier der Median der Daten als horizontale Linie in der Box. Der Median gibt die Mitte der Daten wieder, d.h. die Hälfte der Werte ist größer als der Median und die andere Hälfte kleiner.
Gezeigt ist hier der Median der Daten als horizontale Linie in der Box. Der Median gibt die Mitte der Daten wieder, d.h. die Hälfte der Werte ist größer als der Median und die andere Hälfte kleiner.  Man kann in diesem Violinplot erkennen, dass das Gewicht der unbehandelten Tiere ziemlich uniform um den Mittelwert (weißer Punkt) verteilt ist. Bei den behandelten Tiere sieht man zwei Bäuche in der Verteilung, d.h. es gibt eine Häufung von Daten einmal im oberen und einmal im unteren Wertebereich.
Man kann in diesem Violinplot erkennen, dass das Gewicht der unbehandelten Tiere ziemlich uniform um den Mittelwert (weißer Punkt) verteilt ist. Bei den behandelten Tiere sieht man zwei Bäuche in der Verteilung, d.h. es gibt eine Häufung von Daten einmal im oberen und einmal im unteren Wertebereich. Dies ist gleichzeitig die Darstellung mit dem größten Informationsgehalt. Allerdings kann man sich vorstellen, dass die Darstellung der einzelnen Datenpunkte schnell sehr unübersichtlich wird, wenn über 30-50 Punkte in jeder Gruppe darzustellen sind.
Dies ist gleichzeitig die Darstellung mit dem größten Informationsgehalt. Allerdings kann man sich vorstellen, dass die Darstellung der einzelnen Datenpunkte schnell sehr unübersichtlich wird, wenn über 30-50 Punkte in jeder Gruppe darzustellen sind.
 An diesem Beispiel sieht man, dass der Schweregrad sich kaum zwischen behandelt und unbehandelten Tieren unterscheidet. Auch wenn man sich nur die Behandelten betrachtet erklärt der Schweregrad nicht die beiden Gewichtsgruppen, wohl aber das Geschlecht. Zur Absicherung dieser Aussagen würde man natürlich die passenden statistischen Tests durchführen. Das soll aber hier nicht Thema sein.
An diesem Beispiel sieht man, dass der Schweregrad sich kaum zwischen behandelt und unbehandelten Tieren unterscheidet. Auch wenn man sich nur die Behandelten betrachtet erklärt der Schweregrad nicht die beiden Gewichtsgruppen, wohl aber das Geschlecht. Zur Absicherung dieser Aussagen würde man natürlich die passenden statistischen Tests durchführen. Das soll aber hier nicht Thema sein.